Yan Cui
I help clients go faster for less using serverless technologies.
This article is brought to you by
Save money on RDS by moving your dev environments to Neon serverless Postgres, with instant scaling, scaling to zero (and only 500ms cold start!), and the ability to branch your database as easily as creating a Git branch.
Problem
There are exactly ten ways of selecting three from five, 12345:
123, 124, 125, 134, 135, 145, 234, 235, 245, and 345
In combinatorics, we use the notation, 5C3 = 10.
In general,
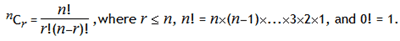
It is not until n = 23, that a value exceeds one-million: 23C10 = 1144066.
How many, not necessarily distinct, values of nCr, for 1 <= n <= 100, are greater than one-million?
Solution
1 2 3 4 5 6 7 8 9 | let factorial n = if (n = 0I) then 1I else [1I..n] |> List.reduce (*)let C n r = if r <= n then (factorial n) / ((factorial r) * (factorial (n - r))) else 0Ilet answer = [1I..100I] |> List.collect (fun n -> [1I..n] |> List.map (fun r -> C n r)) |> List.filter (fun x -> x > 1000000I) |> List.length |
Whenever you’re ready, here are 3 ways I can help you:
- Production-Ready Serverless: Join 20+ AWS Heroes & Community Builders and 1000+ other students in levelling up your serverless game. This is your one-stop shop for quickly levelling up your serverless skills.
- I help clients launch product ideas, improve their development processes and upskill their teams. If you’d like to work together, then let’s get in touch.
- Join my community on Discord, ask questions, and join the discussion on all things AWS and Serverless.