Yan Cui
I help clients go faster for less using serverless technologies.
This article is brought to you by
The real-time data platform that empowers developers to build innovative products faster and more reliably than ever before.
Problem
The square root of 2 can be written as an infinite continued fraction.
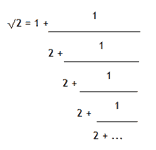
The infinite continued fraction can be written, ?2 = [1;(2)], (2) indicates that 2 repeats ad infinitum. In a similar way, ?23 = [4;(1,3,1,8)].
It turns out that the sequence of partial values of continued fractions for square roots provide the best rational approximations. Let us consider the convergents for ?2.
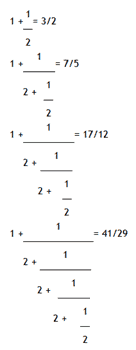
Hence the sequence of the first ten convergents for ?2 are:
1, 3/2, 7/5, 17/12, 41/29, 99/70, 239/169, 577/408, 1393/985, 3363/2378, …
What is most surprising is that the important mathematical constant,
e = [2; 1,2,1, 1,4,1, 1,6,1 , … , 1,2k,1, …].
The first ten terms in the sequence of convergents for e are:
2, 3, 8/3, 11/4, 19/7, 87/32, 106/39, 193/71, 1264/465, 1457/536, …
The sum of digits in the numerator of the 10th convergent is 1+4+5+7=17.
Find the sum of digits in the numerator of the 100th convergent of the continued fraction for e.
Solution
If you look at the convergents of ?2 and the numerators in the convergents of e, you’ll see a pattern emerging:
1 + 2 * 1 = 3
2 + 3 * 2 = 8
3 + 8 * 1 = 11
8 + 11 * 1 = 19
11 + 19 * 4 = 87
If you look at the sequence of numerators in the convergents of e ( 2, 3, 8, 11, … ) and the sequence of numbers in the convergents of ?2 ( 1, 2, 1, 1, 4, 1, … ), given the current numerator ( n ) and the previous numerator ( n-1 ) in the sequence and the corresponding number in the convergents of ?2 ( i )the next numerator ( n+1 ) can be calculated using the formula:
( n+1) = ( n-1 ) + n * i
Once we have this formula to work with, the rest is simple, the solution runs in 7 milliseconds on my machine.
Whenever you’re ready, here are 4 ways I can help you:
- Production-Ready Serverless: Join 20+ AWS Heroes & Community Builders and 1000+ other students in levelling up your serverless game. This is your one-stop shop for quickly levelling up your serverless skills.
- Do you want to know how to test serverless architectures with a fast dev & test loop? Check out my latest course, Testing Serverless Architectures and learn the smart way to test serverless.
- I help clients launch product ideas, improve their development processes and upskill their teams. If you’d like to work together, then let’s get in touch.
- Join my community on Discord, ask questions, and join the discussion on all things AWS and Serverless.