
Yan Cui
I help clients go faster for less using serverless technologies.
Note: see the rest of the series so far.
I stumbled across this post the other day and problem 2 seems like something I can easily do in APL since it essentially requires you to interleave two arrays.
The problem is:
Write a function that combines two lists by alternatingly taking elements. For example: given the two lists [a, b, c] and [1, 2, 3], the function should return [a, 1, b, 2, c, 3].
Here’s the solution I have come up with:
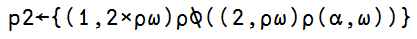
since it uses both $latex \omega$ (right argument) and $latex \alpha$ (left argument) so it’s a dyadic function, let’s test it out:
$latex ‘a’ \ ‘b’ \ ‘c’ \ p2 \ 1 \ 2 \ 3$
=> a 1 b 2 c 3
Here’s how it works:
- concatenate the two arguments together, with the left argument first $latex (\alpha, \omega)$
- reshape $latex \rho$ the concatenated vector into 2 rows, so that you have effectively placed $latex \alpha$ and $latex \omega$ into a matrix, i.e.
$latex
a \ b \ c\\*
1 \ 2 \ 3$
- transpose that matrix
$latex
a \ 1\\*
b \ 2\\*
c \ 3$
- reshape $latex \rho$ the transposed matrix into a vector, and that’s it!
Whenever you’re ready, here are 3 ways I can help you:
- Production-Ready Serverless: Join 20+ AWS Heroes & Community Builders and 1000+ other students in levelling up your serverless game.
- Consulting: If you want to improve feature velocity, reduce costs, and make your systems more scalable, secure, and resilient, then let’s work together and make it happen.
- Join my FREE Community on Skool, where you can ask for help, share your success stories and hang out with me and other like-minded people without all the negativity from social media.

You might be interested in http://dfns.dyalog.com/n_ripple.htm and Dyalog’s #onelinerwednesday take on this problem (see https://twitter.com/dyalogapl/status/575647945032335361).
There was also a T-Shirt with this on in the 80s for the really stylish APLer :-) https://twitter.com/dyalogapl/status/576047693811826688
Assuming that you have only vectors, my solution to this would be `,?,??`.
Strictly speaking your result is a one row matrix rather than a vector. If it’s truly a vector that you want, then your code can be simplified by using ravel rather than reshape (and some of the parentheses can be removed too):
s1?{,?(2,??)??,?}
These days I prefer to use the monadic function Tally (?) rather than monadic ?: Tally returns the length of the leading axis, which in the case of a vector is its length. Tally has the benefit of always returning a scalar.
s2?{,?(2,??)??,?}
A more traditional solution would be to use Catenate (,) with fractional axis:
s3?{,?,[?io+.5]?}
although unless you use the slightly awkward ?io+.5 the expression is ?IO dependent.
Recent versions of Dyalog include Table (?) which has been in Sharp APL and J for many years. Using Table allows the following solution:
s4?{,?,??}
The last expression is the fastest, but as to which is “best” .. well that is in the eye of the beholder !
that’s amazing ;-)
Thanks for these, that’s one of the things I like above APL – there’s always so many different ways to approach a given problem!
Thanks Fiona :-)
Now that we have function trains, I like:
s5?,,[1.5]