Dart – Emulating F#’s Discriminated Union (i.e. an algebraic data type)

Algebraic Data Type

An algebraic data type is a basically a composite type that is formed by combining other types, sometimes also referred to as “sums-and-products” data structures (don’t worries if this is too abstract for you, examples are coming).

A simple example would be a composite type that represents a binary tree that has:

• Nodes – which contains a value and two children, or
• Leaves – which contains a value but no children

Using F#’s discriminated unions we can create a generic Tree type that are composed of two subtypes, Leaf and Node, each with a different set of associated types. We can then use pattern matching to help us retrieve the information about the subtypes when we’re given an instance of Tree.

(note : in F# the types in a tuple is separated by *, so a Node contains a tuple of type T, Tree<T> and Tree<T>).

 

Let’s break down the definition for the Tree type to reveal the three building blocks for algebraic expressions that we can use to describe data structures – sums, products, and recursions (this SO answer has a nice explanation for this).

From here you can build more complicated types (an abstract syntax tree is another common example) using these simple building blocks.

 

Emulating in C#

Now, since C# does not have support for these sum (or union) types, what can you do with discriminated union types that you have created in F#?

Turns out, you can do a pretty good approximation in C# using a class hierarchy instead, although you do lose many of the expressiveness (the succinct syntax for declaring them, and the ability to pattern match against them) you get in F#. The good news is that the F# compiler does most of the heavy lifting for you already.

For each of the union types (i.e. variants of the base type, in the case of Tree, the union types are Leaf and Node) the F# compiler generates a static Tree.NewXYZ method for creating a new instance of that union type, and you can check which union type an instance belongs to by either:

• performing a type test, or
• using the generated IsXYZ property on every instance of Tree

 

For the Tree type we defined in F#, we can create and traverse it using the following:

(note: in C# tuple members are accessed by the ItemX properties where X is the 1-based index of the element.)

 

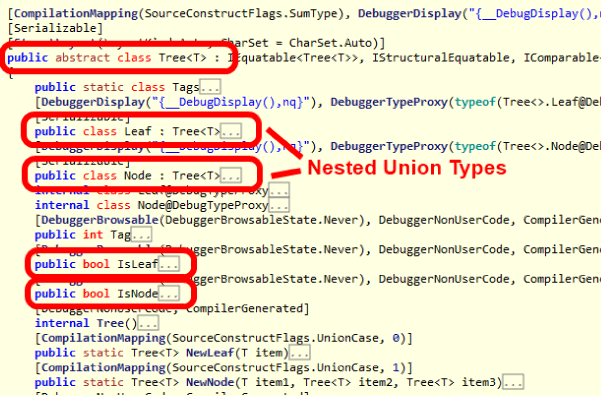
What has happened behind the scene is that the F# compiler has transformed the Tree type we defined into a simple class hierarchy consisting of:

• An abstract Tree<T> type
• Two nested types Leaf and Node which extends from Tree<T>

Peeping at the IL generated by the F# compiler through ILSpy you will find something along the lines of:

 

Emulating in Dart

Now, unfortunately there’s no native support for sum (or union) types in Dart either, but as we saw in the C# case, you can do a pretty good approximation even without it. As an example, here’s how you might define the Tree type in Dart:

In this example, we have an abstract (so you can’t instantiate it with the new keyword) Tree type which is extended by the union types Leaf and Node. Because both Leaf and Node specifies only a private constructor (as denoted by the _ prefix to its named constructor) so the only way to instantiate them is through the static Tree.NewLeaf and Tree.NewNode methods.

Also, note that the private constructors for Leaf and Node calls Tree’s private constructor in order to initialize the isLeaf and isNode public fields.

To use this Tree type, our code is very similar to the C# example:

Here, we need to check whether a given Tree instance is a Leaf or a Node and cast it to the appropriate type (using our helper methods) before we can access the relevant data for each of the union types.

 

On a side note, I stumbled across an interesting library for defining extractors in Dart, so that you get similar pattern matching capabilities as those found in a number of functional languages such as F# and Scala.

 

Related Links

F# – Enums vs Discriminated Unions

F# – Serializing F# record and Discriminated Union types

F# – Use Discriminated Unions instead of class hierarchies

SO – what are ‘sums-and-products’ data structures?

Pattern Matching Combinators for Dart