Advent of Code F# – Day 13

The source code for this post (both Part 1 and Part 2) is available here and you can click here to see my solutions for the other Advent of Code challenges.

Description for today’s challenge is here.

 

The input for Day 13 looks like the following:

Alice would lose 2 happiness units by sitting next to Bob.

Alice would lose 62 happiness units by sitting next to Carol.

Alice would gain 65 happiness units by sitting next to David.

Bob would gain 93 happiness units by sitting next to Alice.

Bob would gain 19 happiness units by sitting next to Carol.

Bob would gain 5 happiness units by sitting next to David.

…

So first, let’s parse the important information out of each line:

• who (x)
• sitting next to whom (y)
• how much does the happiness change as result

we can then build up a Map of this information.

For convenience sake, let’s also create a type alias for this Map, and let’s call it a Graph.

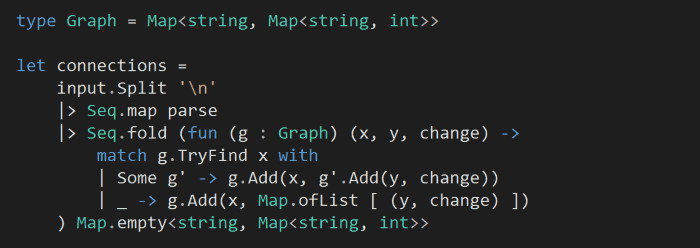
You might have noticed that, where x is found in the graph, we’re using Add to update both the inner and outer Map. This might seem odd/suspicious, but whilst it’s not mentioned in the documentation the behaviour of Add is actually ‘add or update’ – try this in the F# REPL to see for yourself:

> let m = Map.ofList [ 1, “1”];;

val m : Map<int,string> = map [(1, “1”)]

> m.Add(1, “2”);;

val it : Map<int,string> = map [(1, “2”)]

Once we have parsed the input into a ‘graph’, let’s find all possible sitting arrangements:

For each arrangement, we’ll need to score it based on the total happiness of the people in this arrangement:

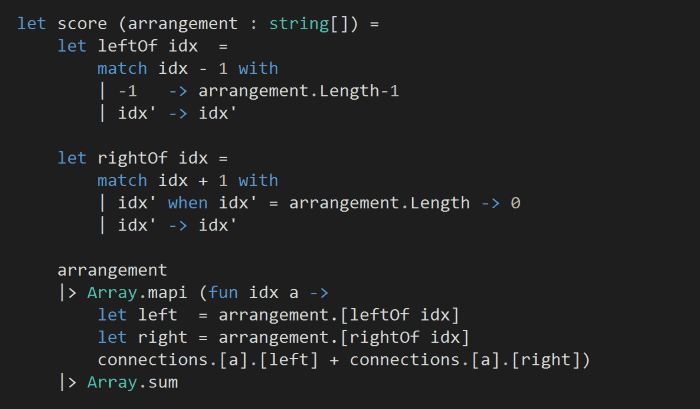
The tricky thing here is to deal with mismatch between the actual sitting arrangement – where everyone sits in a circle – to our representation of it as an array. Which is why I created leftOf and rightOf functions to deal with cases when the index has under/overflown.

Finally, just score every arrangements and find the highest score:

 

Part 2

After considering a few approaches, I decided it’ll be easiest to just modify the input so that all the downstream code we wrote for Part 1 would still work just fine.

So, we first need to know who are all the people that will be sitting at the table:

so we can inject additional lines (bi-directionally) into the input: