Currying vs Partial Application

Recently I have come across some really interesting questions and debates around these two terms and how they differ from one another. There seems to be widespread confusions with many examples demonstrates one whilst intends another, and some simply uses the terms interchangeably.

Whilst admittedly not being a function programming expert, I’ve spent a bit of time scouring the web for information from those who are and I think I’ve finally come to understand the difference between the two!

In case you’re not familiar with what Currying and Partial Application means, here’s some quick definitions for you.

Definitions

Currying

According to Wikipedia, currying is:

the technique of transforming a function that takes multiple arguments in such a way that it can be called as a chain of functions each with a single argument.

This means for a given function f, which takes three parameters x, y, and z and returns R:

f(x, y, z) => R

once curried it becomes:

curriedf(x) => g(y) => h(z) => R

When you supply x to the curried function curriedf, you get back a new function g, g takes a single parameter and returns another function h which also takes a single parameter but this time returns R.

So to get the full application of the original function f, you need to call

curriedf(x)(y)(z).

With currying, parameters must be supplied from left to right starting from the left-most parameter.

Partial Application

Again, borrowing from Wikipedia, Partial applications refers to:

the process of fixing a number of arguments to a function, producing another function of smaller arity.

This means for a given function f, which takes three parameters x, y, and z and returns R:

f(x, y, z) => R

If you fix the first parameter x to 1 then you get another function g that takes two parameters and returns R:

g(y, z) => R    <=>    f(1, y, z) => R

Equally if you fix both x and y to values 1 and 2 respectively then you get another function h that takes one parameter and returns R:

h(z) => R    <=>    f(1, 2, z) => R

Currying vs Partial Application

At first glance the similarities are hard to miss, and one might be tempted to suggest (well, many have!) that they are two of the same thing or that one is simply a special case of the other. However, there are some crucial differences between the two which ultimately dictates their very different applications in practice.

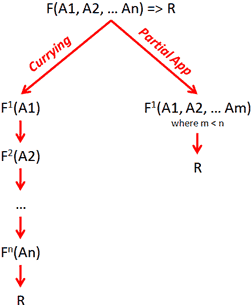To help you understand the differences, try and ignore the fact that both Currying and Partial Application takes a function and returns a function with less input parameters and instead think about the function that’s returned (see image):

Currying

– when you curry a function F, you get back a chain of functions that returns another function at every stage, except the last function in the chain

– you still have to apply all the necessary parameters if you want to get the full application of the original function (i.e. R)

– you have to supply parameters one at a time to a chain of functions

– you have to supply parameters from left to right in the same order as the original function F

Partial Application

– when you partially apply a function F, you get back a function that allows you to get the full application (i.e. R) of the original function F with less parameters

– you don’t have to supply parameters in any particular order

Examples

So, the main difference between currying and partial application lies in the return type of the new function produced, let’s see how they differentiate in practice with a simple example in Javascript:

// original function that takes three parameters a1, a2 and a3
function f(a1, a2, a3) {
    return a1 + a2 + a3;
}

// curried function which takes one parameter at a time
function curry(a1) {
    // each stage takes another parameter and get you closer to the
    // full application of f
    return function (a2) {
        // but only with the inner most function do you actually get
        // the return value you wanted
        return function (a3) {
            return f(a1, a2, a3);
        };
    };
}

// partial applied function which takes one parameter and fixes
// the other 2
function partial(a1) {
    // a partially applied function of the original function f can
    // get you the full application straight away
    return f(a1, 5, 10);

}

curry(1)(5)(10); // returns 16
partial(1); // returns 16

Parting thoughts…

In general, both techniques produce reusable, helpful functions which fixes some parameters of the original function. For example, with Currying the function returned at each and every stage of the chain can be reused and potentially create a tree of functions:

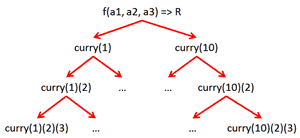
though in practice I can think of few examples where you would require such level of reusable functions…

I’m of the opinion that Partial Application has greater applications (not pun intended!) in solving real world problems. In fact, using Partial Application is something we’ve all done before – e.g. take a general purpose function which needs lots of parameters and make a more high level function out of it by fixing some parameters with sensible defaults:

// base method which provides a way to encapsulate common logic, but
// needs a number of parameters in order to 'tune' its behaviour
// NOTE: this C# code won't compile, it's just to illustrate a common
// pattern of using partial application
public void DoFileIoOperation(
    FileReadWriteMode mode,
    string path, string content,
    FileOverwriteMode overwriteMode)
{
    …
}

// high level methods more useful to anyone who's trying to get things done
public void DoFileRead(string path)
{
    DoFileIoOperation(
        FileReadWriteMode.Read, path, null, FileOverwriteMode.None);
}

public void DoFileWrite(string path, string content)
{
    DoFileIoOperation(
        FileReadWriteMode.Write, path, content, FileOverwriteMode.Overwrite);
}

Also, the fact that you don’t need to supply each and every parameters one at a time, in a particular order makes Partial Application easier to apply in practice. As much as one would love to stay ‘pure’, it’s simply far more pragmatic to repackage the original function signature and fix multiple parameters in one go!