The source code for this post is available here and you can click here to see my solutions for the other Advent of Code challenges.
Description for today’s challenge is here.
It’s the last day of the advent calendar, and today’s challenge appears difficult at first but mostly because of the grid system it imposes upon you.
But after some thought, the problem can be drastically simplified.
Given this grid system:
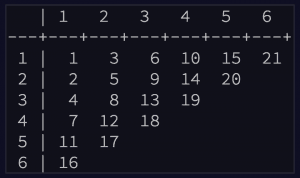
we can work out the one-based index for row N, column 1 in this formula:
F N = F(N-1) + (N-1) where F 1 = 1, F 2 = 2
e.g.
F 2 = 2,
F 3 = F 2 + (3 – 1) = 2 + 2 = 4
F 4 = F 3 + (4 – 1) = 4 + 3 = 7
…
From here, column M is (M – 1) distance away from the first element on the same row and (M – 1) distance away from the row N that marks the start of the diagonal:
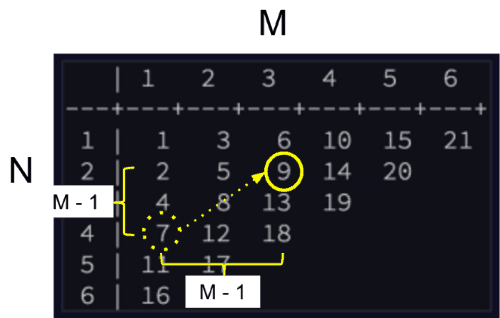
So, the one-based index for row N, column M can be expressed in terms of the F function above:
G (M, N) = F (N + M – 1) + (M – 1)
e.g.
G (3, 2) = F (2 + 3 – 1) + (3 – 1) = F 4 + 2 = 7 + 2 = 9
G (6, 1) = F (1 + 6 – 1) + (6 – 1) = F 6 + 5 = 16 + 5 = 21
…
So for my puzzle input of row 2981, column 3075, it translates = G (3075, 2981)th element where the first element is 20151125.
Taking all these into account, and translating G (M, N) into an (x, y) based system, we can have the following to solve today’s challenge:
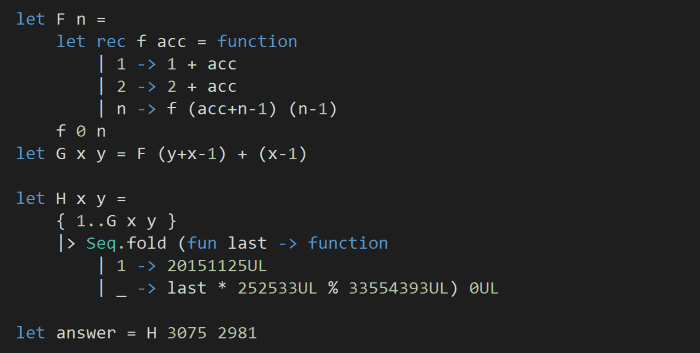
Pretty straightforward, right? Well, the only caveat is how we implemented F here, this is only because I wanted the implementation to be tail recursive, otherwise it can be simple as:
let F = function | 1 -> 1 | 2 -> 2 | n -> F (n-1) + (n-1)
So that’s it folks! We’ve completed all the Advent of Code challenges for 2015, and our F# xmas tree is up and running in all its glory 
