Yan Cui
I help clients go faster for less using serverless technologies.
This article is brought to you by
Don’t reinvent the patterns. Catalyst gives you consistent APIs for messaging, data, and workflow with key microservice patterns like circuit-breakers and retries for free.
The source code for this post (both Part 1 and Part 2) is available here and you can click here to see my solutions for the other Advent of Code challenges.
Description for today’s challenge is here.
The input for Day 9 looks like this:
AlphaCentauri to Snowdin = 66
AlphaCentauri to Tambi = 28
AlphaCentauri to Faerun = 60
Snowdin to Tambi = 22
Snowdin to Faerun = 12
…
there are similarities between this challenge and Day 7 in that they’re essentially a graph problem. In that case, let’s model this problem as a graph:
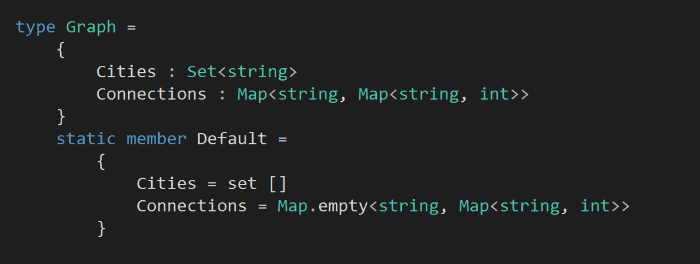
in our model of this problem, we have a set of cities, and the connections between them (where the key is the city to travel from, and the value is a map of the cities that you can travel to and the distance between the pair).
Like we did in Day 7, let’s add a helper function to help connect two cities – a and b – together, along with the distance between them.
Armed with the above, we can now go back to our input, parse each line into two cities and their distance, and then fold over them to build up a graph:
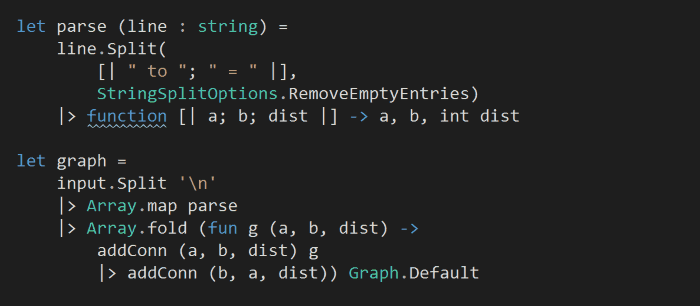
notice that the information we get from the input list is actually bi-directional, which is why in the fold we have to add the direction from a to b, as well as from b to a.
Next, starting with each cities, we want to find the routes that’ll visit each city once and only once.
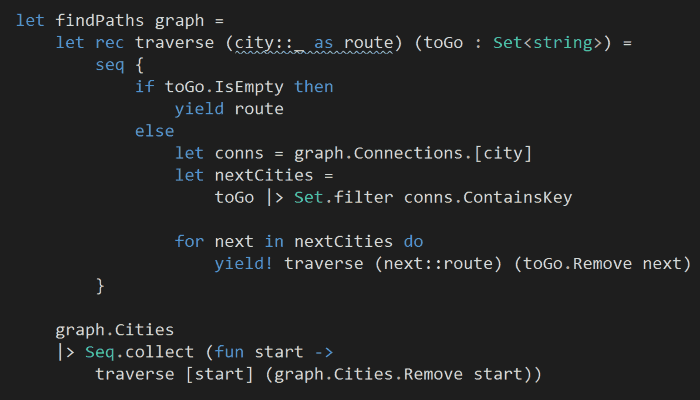
aside: in hindsight, both the model and the path finding algorithm here can be simplified, I simply didn’t realise the distance data is bi-directional (it was implied through the example which I skimmed over and got started writing code…). For instance, the data is set up such that every city is connected to every other city, so the steps I have taken above to determine ‘which cities can I travel from here’ is redundant.
That said, I decided to keep the solution as it is because:
a) it can solve a more general problem where cities do not form a mesh network
b) it works, and pretty easy to understand, so why change 
The last building block we need to compose our final solution is the ability to calculate the total distance we have to travel in a route:
and to answer the challenge:
in hindsight, it might be better to write the above as:
graph |> findPaths |> Seq.map calcDistance |> Seq.min
Part 2
To work out the longest distance one can travel, simply flap the last line to look for the max distance instead, simple:
Whenever you’re ready, here are 3 ways I can help you:
- Production-Ready Serverless: Join 20+ AWS Heroes & Community Builders and 1000+ other students in levelling up your serverless game. This is your one-stop shop for quickly levelling up your serverless skills.
- I help clients launch product ideas, improve their development processes and upskill their teams. If you’d like to work together, then let’s get in touch.
- Join my community on Discord, ask questions, and join the discussion on all things AWS and Serverless.