Project Euler – Problem 83 Solution

The problem description is here, and click here to see all my other Euler solutions in F#.

This is a more difficult version of problem 82, and now you can move in all four directions!

As before, we start by loading the input data into a 2D array:

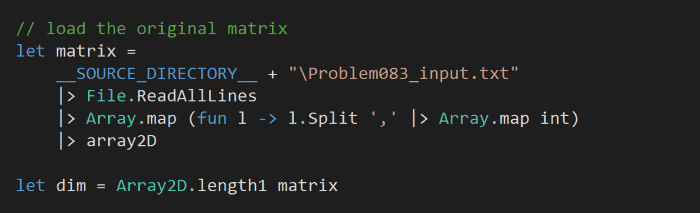
and initialize another matrix of the same size to hold the minimum sum leading to each cell:

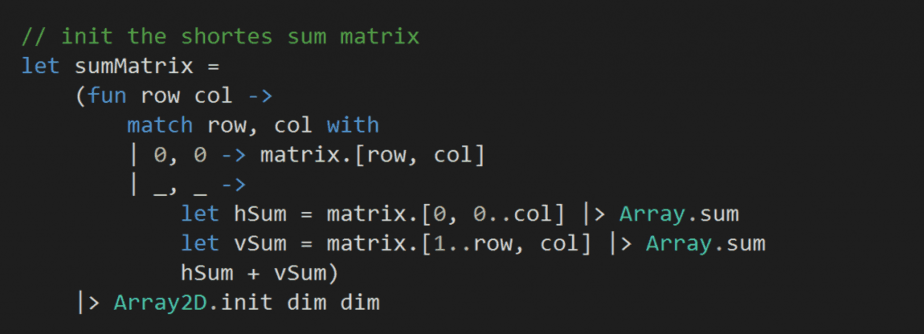
What we have done differently this time though, is to choose initial defaults:

• for the top-left corner (0, 0) the minimum sum is itself
• for all other cells at (row, col) we’ll always traverse right and then down
  • if row = 0, then this equates to only move right until we reach col
  • if col = 0, then this equates to only move down until we reach row

e.g.

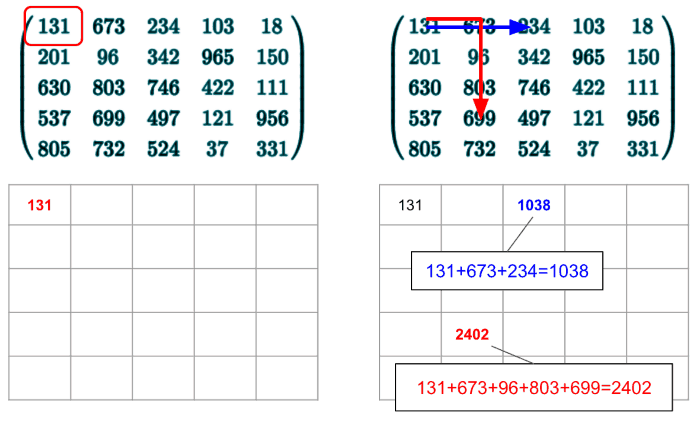
Next, as we did for the problem 82, we’ll add a couple of helper to help us traverse both matrices:

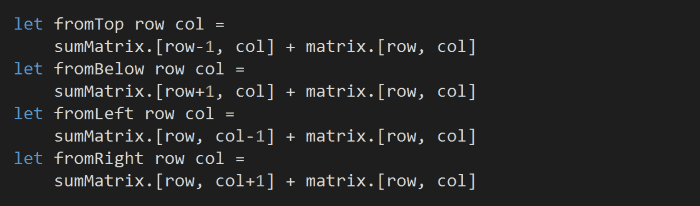
and we’ll find the new minimum sum to each cell by taking the minimum from the four directions:

Unlike before, we can’t isolate to optimizing one column at a time, and instead we’ll need to traverse the whole matrix. For better cache locality, we’ll traverse row first and recursively optimize the whole matrix until no more optimization is possible:

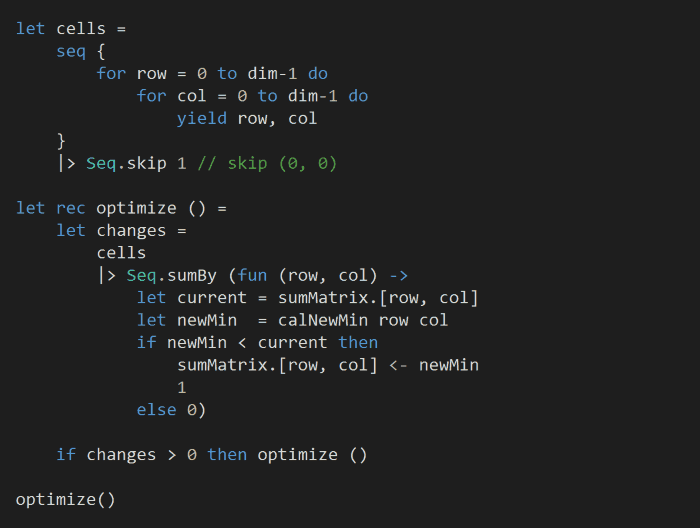
Finally, find the final value for the bottom-right corner of the sum matrix:

This solution runs in 73ms on my laptop.

The source code for this solution is here.