Project Euler – Problem 82 Solution

The problem description is here, and click here to see all my other Euler solutions in F#.

 

This is a more difficult version of problem 81, but still, as you can’t move left so we can still optimize one column at a time.

First, let’s read the input file into a 2D array:

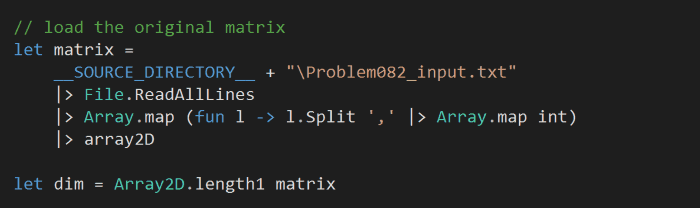
and initialize another matrix with the same size to store the minimum sum to each of the cells:

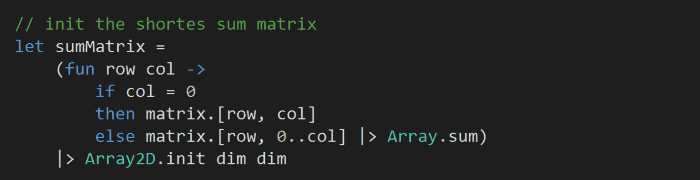
In order to avoid miscalculations due to uninitialized cells (i.e. if we had initialized them with 0), I’ve initialized the cells by assuming that we have moved right all the way, hence this line:

    else matrix.[row, 0..col] |> Array.sum

which adds up all the cells to the left of, and including, the (row, col) cell.

Next, we’ll add a couple of helper functions to work out the new minimum sum to the cell at (row, col) if we had moved up, down, or right:

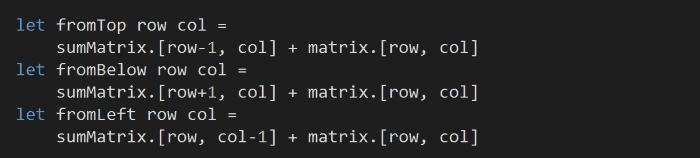
We can now use these functions to optimize the columns one at a time.

The tricky thing here is that we might need a few passes to converge onto the true minimum sum path to each of the cells. For example, in order to work out the minimum sum at (row, col) we need to know the minimum sum at (row-1, col) and (row+1, col). But to work out the minimum sum at (row-1, col) we need to know the minimum sum at (row, col)!

So, instead, we’ll recursively try to optimize each cell in the column until it can’t be optimized anymore:

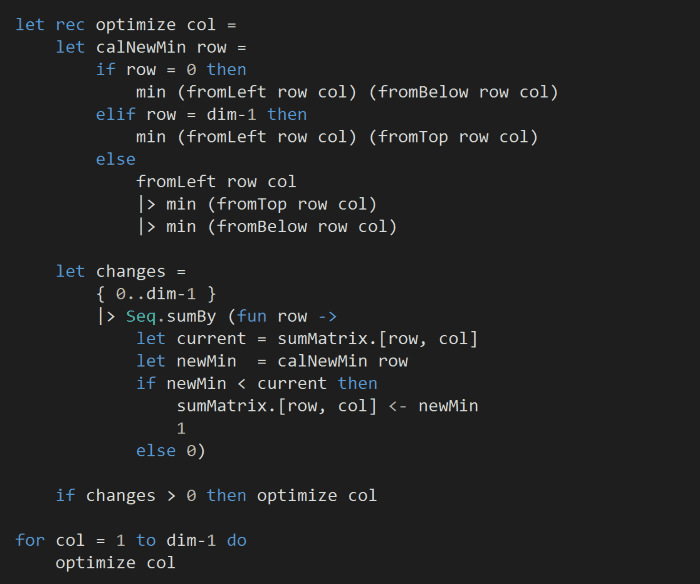
At the end of the snippet above, we optimized the columns one at a time from left to right. (I could have equally included this as part of the recursive function, but it would introduce another level of nesting which is why I opted against it)

And finally, look for the minimum sum on the right-most column in the sum matrix to answer the question:

This solution runs in 9ms on my laptop.

 

The source code for this solution is here.