Project Euler – Problem 57 Solution

Problem

It is possible to show that the square root of two can be expressed as an infinite continued fraction.

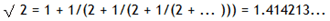
By expanding this for the first four iterations, we get:

1 + 1/2 = 3/2 = 1.5

1 + 1/(2 + 1/2) = 7/5 = 1.4

1 + 1/(2 + 1/(2 + 1/2)) = 17/12 = 1.41666…

1 + 1/(2 + 1/(2 + 1/(2 + 1/2))) = 41/29 = 1.41379…

The next three expansions are 99/70, 239/169, and 577/408, but the eighth expansion, 1393/985, is the first example where the number of digits in the numerator exceeds the number of digits in the denominator.

In the first one-thousand expansions, how many fractions contain a numerator with more digits than denominator?

Solution

// define function to return all the numerator-denominator pairs for the first n expand
let expand n =
    Seq.unfold (fun (num, denom) -> Some((num, denom), (denom*2I+num, denom+num))) (3I, 2I)
    |> Seq.take n

let answer =
    expand 1000
    |> Seq.filter (fun (num, denom) -> num.ToString().Length > denom.ToString().Length)
    |> Seq.length

If you look at the patterns 3/2, 7/5, 17/12, 41/29, and so on, it’s easy to spot a pattern where the numerator and denominator of iteration n can be derived from the iteration n-1:

Numerator(n) = Numerator(n-1) + 2 * Denominator(n-1)

Denominator(n) = Numerator(n-1) + Denominator(n-1)