F# – genetic algorithms to help you catch monsters

The monster trapping mechanics in Here Be Monsters is fairly straight forward:

• Monsters have a type and a set of stats – Strength, Speed and IQ
• They have a rarity value which determines the likelihood of an encounter
• They have a set of baits they like, which can increase the likelihood of an encounter
• Traps can catch monsters of matching types
• Traps also have a set of stats – Strength, Speed and Tech
• Chance of catching a monster is determined by the trap’s stats vs the monster’s stats

 

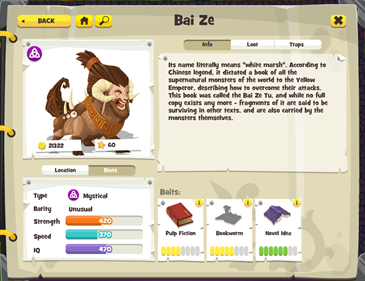
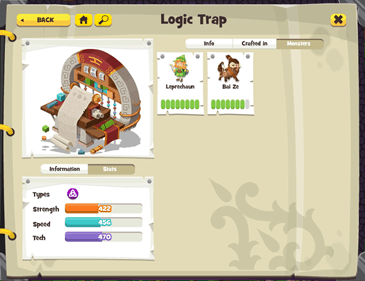
It’s as simple as it sounds. Unless, of course, you’re the game designer responsible for setting the stats for the trap so that:

a. you achieve the intended catch rate % against each of the monsters, and

b. the distribution of the stats should ‘make sense’, i.e. a low-tech box trap should have higher stats in strength than Tech

 

The naive approach would be to start with a guesstimate and then use trial-and-error until you converge upon an answer or an approximation to the answer that is considered good enough. The naive approach would be laborious and error prone, and unlikely to yield the optimal result (barring the Herculean effort of a persistent game designer..).

 

To automate this process and aid our game designers, we designed and implemented a simple genetic algorithm in F# that would search and find the optimal solution based on:

• intended % catch rate for each monster
• an error margin
• an initial set of stats that defines the ideal distribution of stats

The game designers can use our custom web tool to run the algorithm, for example:

 

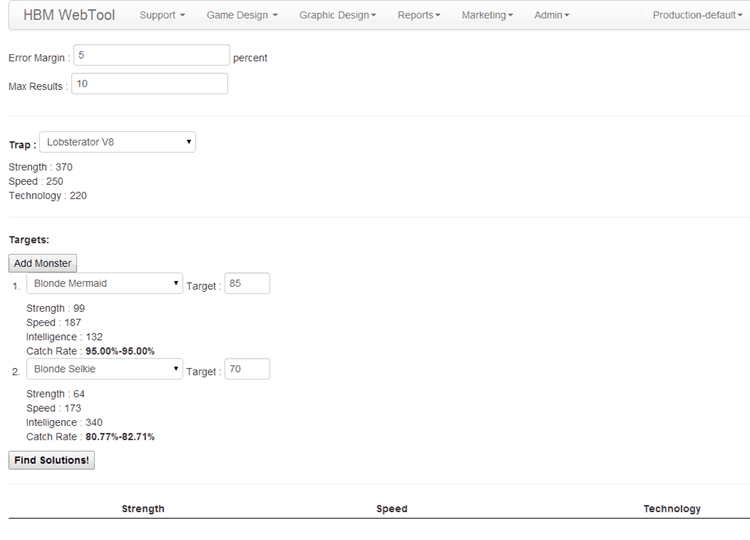
In simple terms, a genetic algorithm starts with a set of potential solutions and iteratively generates new generations of solutions using a selection and a mutation process such that:

• the selection process chooses which of the solutions survive (survival of the fittest and all) based on a fitness function
• the mutation process generates a new solutions using the surviving solutions

the iteration continues until one of the terminations conditions have been met, for example, if a solution is found or we’ve reached the maximum number of generations allowed.

 

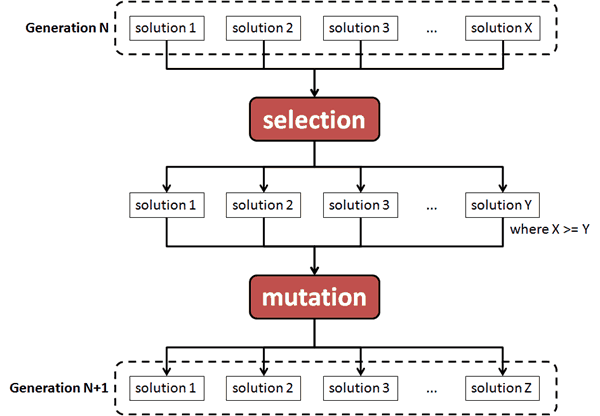
In our algorithm, each solution is a set of stats for the trap, and the selection process calculates the catch rate for each of the monsters using the solution, and keeps the solution if it’s better than the solution it’s mutated from.

The mutation process then takes each of he surviving solutions and generates new solutions by tweaking the stats in a number of ways:

• +/- a small amount from each of Strength/Speed/Tech (generates better solutions when we’re close to optimal solutions)
• +/- a large amount from each of Strength/Speed/Tech (generates noticeably different solutions we’re far from optimal solutions)

So from an initial solution of Strength:100, Speed:100 and Tech:200, you can end up with a number of different solutions for the next generation:

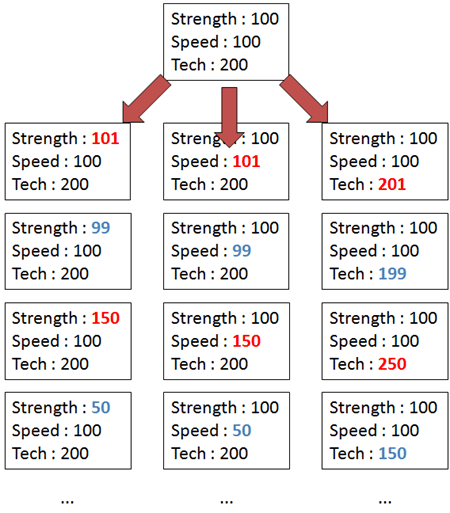
This process continues until either:

• the max number of generations has been exhausted, or
• none of the new solutions survive the selection process

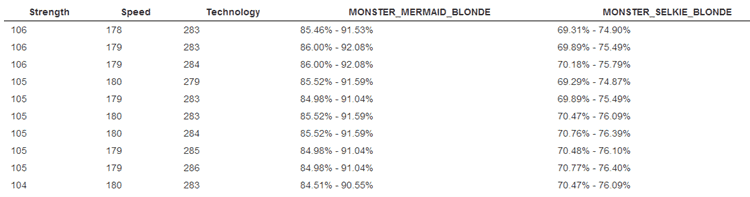
the final survivors are then filtered using the error margin specified by the game designer, and sorted by how close it’s to the specified target catch rates, e.g.

 

We have also applied the same technique and implemented genetic algorithms to:

• find stats for a monster that will give it the intended catch rate for a number of traps (the inverse of the above)
• find configuration for baits so that we can achieve the desired encounter rate with a monster when using this bait (see below for an example)

 

 

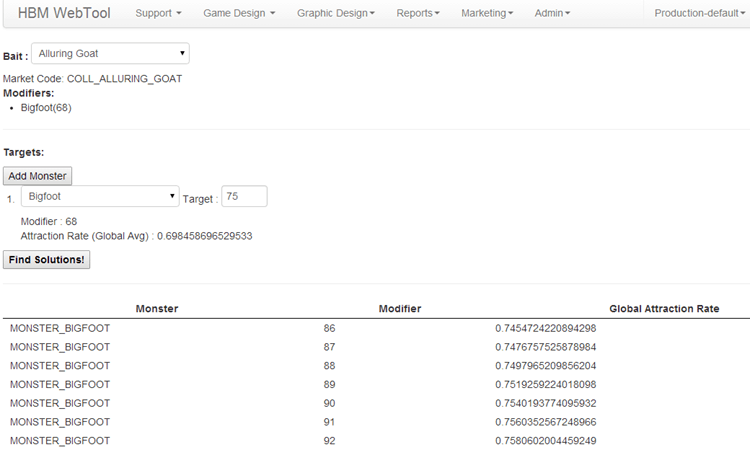
So here you ago, I hope you enjoyed reading about another place where a bit of F# magic has come in handy.

The code for the genetic algorithms is not very complicated (or very long) but incredibly specific to our specific domain, hence the lack of any code snippet in this post. But hopefully I’ve managed to give you at least a flavour of what genetic algorithms are and how you might be able to apply them (with F# if possible!) in your own solution.