
Yan Cui
I help clients go faster for less using serverless technologies.
This article is brought to you by

The real-time data platform that empowers developers to build innovative products faster and more reliably than ever before.
Problem
Triangle, square, pentagonal, hexagonal, heptagonal, and octagonal numbers are all figurate (polygonal) numbers and are generated by the following formulae:
The ordered set of three 4-digit numbers: 8128, 2882, 8281, has three interesting properties.
- The set is cyclic, in that the last two digits of each number is the first two digits of the next number (including the last number with the first).
- Each polygonal type: triangle (P3,127=8128), square (P4,91=8281), and pentagonal (P5,44=2882), is represented by a different number in the set.
- This is the only set of 4-digit numbers with this property.
Find the sum of the only ordered set of six cyclic 4-digit numbers for which each polygonal type: triangle, square, pentagonal, hexagonal, heptagonal, and octagonal, is represented by a different number in the set.
Solution
(see full solution here),
The tricky thing here (at least for me) was to remember that the six 4-digit numbers have to come from different sets, but not necessarily in the order of P3, P4, … P8. Once that is cleared up, the rest is fairly straight forward. In the solution linked above, I first created a set of functions for generating triangle, square, pentagonal, … octagonal numbers:
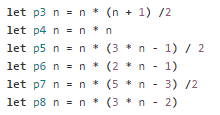
Since the question concerns only 4-digit numbers, so for efficiency sake let’s generate the desired 4 digit numbers ahead of time and safe them for later use:
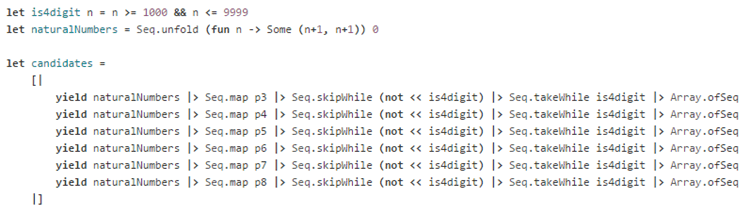
The is4digit predicate function is self-explanatory. naturalNumbers is an infinite sequence of integers starting from 1, we use this sequence to generate the figurate numbers we need, but only keep those that are actually 4 digits.
So far so good, we have all the figurate numbers in an array where [0] => P3, [1] => P4, and so on.
Next, create permutations of the figurate numbers such that we exhaust all possible sequence of figurate numbers:
P3 => P4 => P5 => P6 => P7 => P8
P3 => P4 => P6 => P7 => P8 => P5
P4 => P3 => P5 => P6 => P7 => P8
…
![]()
(P.S. the permute function here comes from the Common.fs source file in the solution)
To find the answer to the problem, we process each permutation to find our answer, take a moment to understand this code:

The processPermutation function processes one permutation of the figurate numbers and the termination conditions for the inner loop function are:
1. we have one number from each figurate number set and that the last 2 digits of the last number = first 2 digits of first number
![]()
2. we have one number from each figurate number set but last 2 digits of last number <> first 2 digits of first number (so close!)
![]()
3. one of the figurate number set in the sequence doesn’t contain a number whose first 2 digits = the last 2 digits of the number selected from the last figurate number set (short-circuited)
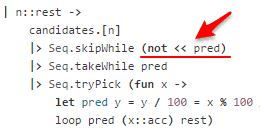
For each number in the current set of figurate numbers we build up a new predicate function – e.g. if x = 1282 then the predicate function would find 4-digit numbers whose first two digit = 82 – and use it to process the next set of figurate numbers in the sequence.
The loop function returns int list option where the int list represents the cyclic figurate numbers we’re looking for, so all that’s left is to unpack the option type and then sum the list.
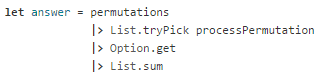
This solution took 17ms to find the solution on my machine.
Whenever you’re ready, here are 4 ways I can help you:
- Production-Ready Serverless: Join 20+ AWS Heroes & Community Builders and 1000+ other students in levelling up your serverless game. This is your one-stop shop for quickly levelling up your serverless skills.
- Do you want to know how to test serverless architectures with a fast dev & test loop? Check out my latest course, Testing Serverless Architectures and learn the smart way to test serverless.
- I help clients launch product ideas, improve their development processes and upskill their teams. If you’d like to work together, then let’s get in touch.
- Join my community on Discord, ask questions, and join the discussion on all things AWS and Serverless.
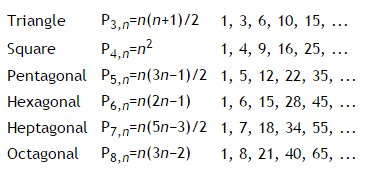
Pingback: Year in Review, 2014 | theburningmonk.com