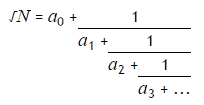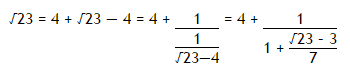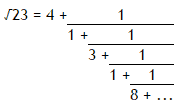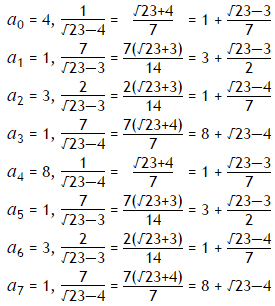Problem
All square roots are periodic when written as continued fractions and can be written in the form:
For example, let us consider ?23:
If we continue we would get the following expansion:
The process can be summarised as follows:
It can be seen that the sequence is repeating. For conciseness, we use the notation ?23 = [4;(1,3,1,8)], to indicate that the block (1,3,1,8) repeats indefinitely.
The first ten continued fraction representations of (irrational) square roots are:
?2=[1;(2)], period=1
?3=[1;(1,2)], period=2
?5=[2;(4)], period=1
?6=[2;(2,4)], period=2
?7=[2;(1,1,1,4)], period=4
?8=[2;(1,4)], period=2
?10=[3;(6)], period=1
?11=[3;(3,6)], period=2
?12= [3;(2,6)], period=2
?13=[3;(1,1,1,1,6)], period=5
Exactly four continued fractions, for N <= 13, have an odd period.
How many continued fractions for N <= 10000 have an odd period?
Solution
(see full solution here).
Based on the algorithm on continued fractions from Wikipedia, we can implement the expansion algorithm as:
From the Wikipedia page:
The algorithm can also terminate on ai when ai = 2 a0, which is easier to implement.
which corresponds to the termination condition we have in the Repeat active pattern (which also checks if the accumulator is empty):
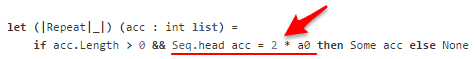
Also, this algorithm doesn’t work on numbers that are perfect squares, i.e. 4, 9, 16, … hence we need to exclude them when searching for our answer.
Here’s the solution in full:
This solution took 92ms to execute on my machine.