Project Euler – Problem 68 Solution

Problem

Consider the following “magic” 3-gon ring, filled with the numbers 1 to 6, and each line adding to nine.

Working clockwise, and starting from the group of three with the numerically lowest external node (4,3,2 in this example), each solution can be described uniquely. For example, the above solution can be described by the set: 4,3,2; 6,2,1; 5,1,3.

It is possible to complete the ring with four different totals: 9, 10, 11, and 12. There are eight solutions in total.

By concatenating each group it is possible to form 9-digit strings; the maximum string for a 3-gon ring is 432621513.

Using the numbers 1 to 10, and depending on arrangements, it is possible to form 16- and 17-digit strings. What is the maximum 16-digit string for a “magic” 5-gon ring?

Solution

(see full solution here)

 

Before we go into details on the solution, let’s first structure the question in a way that’s easy for us to compute.

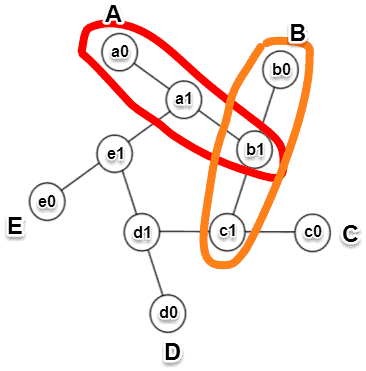
To construct the magic circle, be it for a 3-gon or a 5-gon ring, we can slice up the numbers into pairs – e.g. A => [1; 2], B => [3; 4], C => [5; 6], D => [7; 8], E => [9; 10] – and the problem becomes finding ways in which the numbers can be permuted such that:

1. a0 is the smallest amongst a0, b0, c0, d0, and e0
2. the sums of a0 + a1 + b1, b0 + b1 + c1, … are the same

For example:

 

First, we’ll find the different ways the numbers 1 to 10 can be permuted, and for each permutation slice the numbers into pairs:

(this makes use of a permute function defined in the Common.fs source file in the solution).

 

Then we need a function to sum a pair of number with the last element in the adjacent pair – e.g. a0 + a1 + b1:

 

For each permutation, we need to check:

1. if a0 is the smallest amongst the head elements
2. if the sums of the groups of 3 – i.e. a0 + a1 + b1, b0 + b1 + c1, etc. – are the same

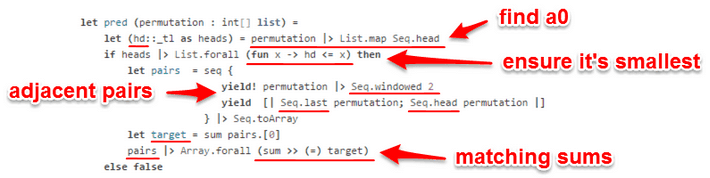
This predicate function allows us to find arrangements that meet our criteria. All that’s left is to turn the result groups of 15 numbers into 16/17-digit strings and find the maximum (see full solution below).

 

Here’s the full solution:

 

This solution took 26s to execute on my machine.