Fear and Loathing with APL

Having heard so much about APL from Phil Trelford (who is one of the leaders in the F# community) I decided to try it out too. For the uninitiated, APL code looks every bit as mind-bending and unbelievable as scenes from Johnny Depp’s Fear and Loathing in Las Vegas.

For example, the life function below implements Conway’s game of life:

$latex life\gets\{\uparrow1 \ \omega\lor.\land3 \ 4=+/,^-1 \ \emptyset \ 1\circ.\ominus^-1 \ \emptyset \ 1\circ.\phi\subset\omega\}&s=2$

I know, right? WTF and mind blowing in equal measures…

 

As I was learning through Mastering Dyalog APL, I took down plenty of notes which I hope will help get you up to speed with the basics quickly.

You can try out the examples at TryAPL, just click on the “APL Keyboard” button and use the virtual keyboard to enter the symbols you need.

Learn APL in 10 Minutes

$latex +$ and $latex -$ does what you’d expect but multiplication and division becomes $latex \times$ and $latex \div$ (just like in maths).

$latex *$ in APL is power, i.e. $latex 7 * 3 = 7 \times 7 \times 7$

/ in APL also means something else, which we’ll come to later.

Also note the difference between negative sign $latex ^-$ and subtraction $latex -$, e.g. $latex 1 – ^-1 = 2$

 

Use $latex \gets$ to assign a value (either scalar or array) to a name, e.g.

$latex X \gets 17.5$

$latex Years \gets 1942 \ 1958 \ 2007$

and remember, variable names are case sensitive.

Variables are mutable, and you can assign multiple variable at once:

$latex X \ Y \ Z \gets 1 \ 2 \ 3$

but only if the length match, otherwise you’ll get an error

$latex X \ Y \gets 1 \ 2 \ 3$

=> $latex LENGTH \ ERROR$

 

You can perform arithmetic operations between two arrays with the same shape:

$latex 1 \ 3 \ 5 \ – \ 3 \ 2 \ 1$

=> $latex ^-2 \ 1 \ 4$

$latex

Price \gets 5.2 \ 11.5 \ 3.6 \ 4.8 \ 4.5 \\*

Qty \gets 2 \ 1 \ 3 \ 6 \ 2 \\*

Price \times Qty$

=> $latex 10.4 \ 11.5 \ 10.8 \ 28.8 \ 9$

look ma, no loops 

If the shape doesn’t match, then you get an error:

$latex 1 \ 3 \ 5 – 3 \ 2$

=> $latex LENGTH \ ERROR$

 

But, if one of the variables is a scalar then the other variable can be any shape:

$latex 1 \ 3 \ 5 – 3$

=> $latex ^-2 \ 0 \ 2$

$latex 3 \times 1 \ 3 \ 5$

=> $latex 3 \ 9 \ 15$

The same rule applies to other operations, e.g. max $latex \lceil$ and min $latex \lfloor$.

$latex 75.6 \ \lceil \ 87.3$

=> $latex 87.3$

$latex 11 \ 28 \ 52 \ 14 \ \lceil \ 30 \ 10 \ 50 \ 20$

=> $latex 30 \ 28 \ 52 \ 20$

$latex 11 \ 28 \ 52 \ 14 \ \lceil \ 30$

=> $latex 30 \ 30 \ 52 \ 30$

 

Most symbols in APL have double meaning, just like they do in algebra, e.g.

$latex a = x – y$ where – means subtraction, a dyadic use of the symbol

$latex a = -y$ where – means negative, a monadic use of the same symbol

(before you freak out, monadic here is of the Mathematics definition, and not the Haskell variant )

To find the length of an array, you can use Rho $latex \rho$ monadically:

$latex

Price \gets 1 \ 2 \ 3 \ 4 \ 5 \\*

\rho Price$

=> 5

 

You can also Rho  $latex \rho$ dyadically to organize items into specified shapes, i.e.

$latex

Tab \gets 4 \ 2 \ \rho \ 25 \ 60 \ 33 \ 47 \ 11 \ 44 \ 53 \ 28 \\*

Tab$

=>

$latex

25 \ 60 \\*

33 \ 47 \\*

11 \ 44 \\*

53 \ 28$

where 4 2 describes the shape – 4 rows, 2 columns, followed by Rho $latex \rho$ and the array of items to be organized.

If the number of items in the array doesn’t match the number of slots in the shape we’re trying to organize into, then the array is repeated, e.g.

$latex 3 \ 2 \ \rho \ 1 \ 2 \ 3 \ 4$

=>

$latex

1 \ 2 \\*

3 \ 4 \\*

1 \ 2$

$latex 3 \ 2 \ \rho \ 1 \ 2$

=>

$latex

1 \ 2 \\*

1 \ 2 \\*

1 \ 2$

If there are too many items then extra items are ignored:

$latex 2 \ 2 \ \rho \ 1 \ 2 \ 3 \ 4 \ 5 \ 6$

=>

$latex

1 \ 2 \\*

3 \ 4$

Utilizing the way items are repeated, there’s a neat trick you can do, e.g.

$latex 3 \ 3 \ \rho \ 1 \ 0 \ 0 \ 0$

=>

$latex

1 \ 0 \ 0 \\*

0 \ 1 \ 0 \\*

0 \ 0 \ 1$

 

In general, APL has special names for data depending on its shape:

scalar – single value

vector – list of values

matrix – array with 2 dimensions

array – generic term for any set of values, regardless of no. of dimensions

table – common term for matrix

cube – common term for array with 3 dimensions

Ok, now that we’ve introduced the notion of dimensions, it’s time to confess that I slightly misled you earlier – Rho $latex \rho$ actually returns the shape of an array (not just its length, which only applies to a vector), so it works with multi-dimensional data too.

$latex \rho (2 \ 2 \ \rho \ 1 \ 2 \ 3\ 4)$

=> 2 2

Furthermore, since the result of Rho $latex \rho$ is itself a vector, applying Rho $latex \rho$ again will give us the number of dimensions an array has – otherwise known as its Rank.

$latex \rho \rho (2 \ 2 \ \rho \ 1 \ 2 \ 3 \ 4)$

=> 2

i.e. scalars have 0 rank, vectors have 1 rank, and so on…

 

You can also reduce over a set of values using / e.g. a plus reduction to sum up all the numbers in an array can be written as

$latex +/ \ 21 \ 45 \ 18 \ 27 \ 11$

=> $latex 122$

similarly, factorial can be written using multiply reduction:

$latex \times/ \ 1 \ 2 \ 3 \ 4 \ 5$

=> $latex 120$

The / symbol is an operator, whereas $latex + \ – \ \times \ \lceil$ etc. are functions. / can accept any of these functions and uses it to reduce over an array.

$latex \lceil/ \ 1 \ 3 \ 5 \ 7 \ 9 \ 6 \ 4 \ 2$

=> 9

$latex \lfloor/ \ 1 \ 3 \ 5 \ 7 \ 9 \ 6 \ 4 \ 2$

=> 1

 

APL calls programs defined functions, and you can create a defined function like this:

$latex

Average \gets \{ (+/ \ \omega) \div \rho \omega \}\\*

Average \ 1 \ 2 \ 3 \ 4 \ 5$

=> 3

where:

$latex Average$ – program name

$latex \omega$ – generic symbol for array passed on the right

$latex \alpha$ – generic symbol for array passed on the left

for example, if we have a function $latex f$ such that

$latex

f \gets \{ (+/ \ \omega) – (+/ \ \alpha) \}\\*

1 \ 2 \ 3 \ f \ 4 \ 5 \ 6 \ 7$

=> 16

what we’ve done here is to sum the array on the right of $latex f$ – 4 5 6 7 – and subtract it with the sum of the array on the left – 1 2 3.

Simple, right? Let’s try a few more.

$latex

Plus \gets \{ \omega + \alpha \}\\*

Times \gets \{ \omega \times \alpha \}\\*

(3 \ Plus \ 6) \ Times \ (2 \ Plus \ 5)$

=> 63

and you can use your custom functions with reduction:

$latex Plus/ \ 1 \ 2 \ 3 \ 4 \ 5$

=> 15

 

To index into an array, you can use the standard [ ] notation:

$latex

Val \gets 1 \ 2 \ 3 \ 4 \ 5\\*

Val[4]$

=> 4

noticed that? APL is one-indexed!

What’s more, just like everything else, you can index into array with either a scalar or an array:

$latex Val[1 \ 3 \ 4]$

=> 1 3 4

$latex Val[1 \ 3 \ 4 \ 1]$

=> 1 3 4 1

This also works when it comes to updating values in an array:

$latex

Val[1 \ 3 \ 5] \gets 42\\*

Val$

=> 42 2 42 4 42

$latex

Val[1 \ 3 \ 5] \gets 1 \ 3 \ 5\\*

Val$

=> 1 2 3 4 5

$latex Val[2 \ 2 \ \rho \ 1 \ 2 \ 3 \ 4] $

=>

$latex

1 \ 2 \\*

3 \ 4$

Note that it follows the same rule as functions with regards to the input being either a scalar or a same-shaped array.

If the shape of the array doesn’t match, then it’ll error:

$latex

Val[1 \ 3 \ 5] \gets 2 \ 4\\*

Val$

=> $latex LENGTH \ ERROR$

Equally, if you use an invalid index, you’ll also get an error:

$latex Val[6]$

=> $latex INDEX \ ERROR$

 

You can use Iota $latex \iota$ to generate an array of integers from 1 to N, e.g.

$latex \iota 4$

=> 1 2 3 4

$latex Val[\iota 4]$

=> 1 2 3 4

 

Booleans are represented as 1 and 0, and you can use any one of these relational functions: < = =/ > $latex \leq$ $latex \geq$

$latex 1 \ 3 \ 5 \ > \ 6 \ 2 \ 4$

=> 0 1 1

$latex 1 \ 3 \ 5 \ < \ 6 \ 2 \ 4$

=> 1 0 0

AND and OR semantics are represented by $latex \land$ and $latex \lor$ respectively.

$latex (1 \ 3 \ 5 > 6 \ 2 \ 4) \land (1 \ 3 \ 5 = 6 \ 3 \ 1)$

=> 1 0 1

$latex (1 \ 3 \ 5 > 6 \ 2 \ 4) \lor (1 \ 3 \ 5 = 6 \ 3 \ 1)$

=> 0 1 1

you can use them to count no. of employees based on salary for instance:

$latex

Salaries \gets 1000 \ 1500 \ 2750 \ 3000 \ 2000\\*

+/ (Salaries > 2500)$

=> 2

 

You can also use an array of boolean values as masks too:

$latex 1 \ 0 \ 1 \ / \ 1 \ 2 \ 3$

=> 1 3

$latex 1 \ 0 \ 1 \ / \ ‘iou’$

=> iu

this is called compression, and is useful for selecting items conforming to some criteria, e.g.

$latex

Val \gets 11 \ 13 \ 1 \ 8 \ 9 \ 15 \ 7\\*

Val > 10$

=> 1 1 0 0 0 1 0

$latex \rho Val$

=> 7

$latex \iota \rho\ Val$

=> 1 2 3 4 5 6 7

therefore, to find the indices of values that’s greater than 10

$latex (Val > 10) \ / \ \iota \rho Val$

=> 1 2 6

and to get the corresponding values, just use compression:

$latex (Val > 10) \ / \ Val$

=> 11 13 15

 

Given two arrays, A and B, you can return a new array with all the elements of A minus all the elements of B using the without operator ~

$latex

A \gets 1 \ 2 \ 3\\*

B \gets 3 \ 4 \ 5\\*

A \sim B$

=> 1 2

this doesn’t modify A or B though.

$latex A$

=> 1 2 3

$latex B$

=> 3 4 5

 

memberships

To find items from an array that exists in another array, you can use the membership operator $latex \epsilon$

$latex (\iota 5) \ \epsilon \ 1 \ 3 \ 5$

=> 1 0 1 0 1

it also works with strings

$latex

Phrase \gets \ ‘Panama \ is \ a \ canal \ between \ Atlantic \ and \ Pacific’\\*

Phrase \ \epsilon \ ‘aeiouy’$

=> 0 1 0 1 0 1 0 1 0 0 1 0 0 1 0 1 0 0 0 1 0 0 1 1 0 0 0 0 0 1 0 0 1 0 0 1 0 0 0 0 1 0 1 0 1 0

you can (like before) get the indices of matches using compression:

$latex (Phrase \ \epsilon \ ‘aeiouy’) \ / \ \iota \rho Phrase$

=> 2 4 6 8 11 14 16 20 23 24 30 33 36 41 43 45

or find the matching characters using compression:

$latex (Phrase \ \epsilon \ ‘aeiouy’) \ / \ Phrase$

=> aaaiaaaeeeaiaaii

inspecting the result tells us that those are indeed the characters we’re looking for!

 

search

We saw how we can combine memberships and iota-rho $latex \iota \rho$ to find the indices in Phrase that corresponds to a member in ‘aeiouy’.

What if we want to find the first index each character in ‘aeiouy’ appears in Phrase, i.e. “aeiouy”.Select(char -> Phrase.IndexOf(char)) if you’re coming from a .Net background.

We can use the dyadic form of Iota $latex \iota$:

$latex Phrase \ \iota \ ‘aeiouy’$

=> 2 20 8 47 47 47

note that the length of Phrase is 46

$latex \rho Phrase$

=> 46

so the result 47 is essentially saying that ‘o’, ‘u’, ‘y’ never appeared in Phrase.

 

You can model an ‘else’ semantic using two arrays whose lengths are off by 1. For instance:

$latex

Area \gets \ 17 \ 50 \ 59 \ 84 \ 89\\*

Discount \gets \ 9 \ 8 \ 6 \ 5 \ 4 \ 2$

based on the way search works (not found = length + 1), we can map the specified Area codes to corresponding discount rates: 17 -> 9, 50 -> 8, … 89 -> 4, and all others to 2.

$latex

D \gets \ 24 \ 75 \ 89 \ 60 \ 92 \ 50 \ 51 \ 50 \ 84 \ 66 \ 17 \ 89\\*

Area \ \iota \ D$

=> 6 6 5 6 6 2 6 2 4 6 1 5

so where D does not exist in Area, you’ll get index 6 which does not exist in Area, BUT exists in Discount – i.e. the ‘other’ case we’re trying to model.

So if we use the result of $latex Area \ \iota \ D$ as indices in Discount we’ll find the corresponding discount rate for the values in D:

$latex Discount[Area \ \iota \ D]$

=> 2 2 4 2 2 8 2 8 5 2 9 4

this is an algorithm for changing the frame of reference, i.e. changing a list of area codes into a list of discount values, a general form can be described as:

$latex FinalSet[InitialSet \ \iota \ Values]$

where $latex \rho FinalSet$ = $latex \rho InitialSet$ + 1

 

take and drop

You can use the Take $latex \uparrow$ and Drop $latex \downarrow$ functions like you do with Enumerable.Take and Enumerable.Drop in LINQ:

$latex

L \gets \iota 10\\*

4 \ \uparrow \ L$

=> 1 2 3 4

$latex 4 \ \downarrow \ L$

=> 5 6 7 8 9 10

if the count is negative then you take from the end of the list, e.g. take last 3 items or drop last 7 items:

$latex ^-3 \ \uparrow \ L $

=> 8 9 10

$latex ^-7 \ \downarrow \ L$

=> 1 2 3

 

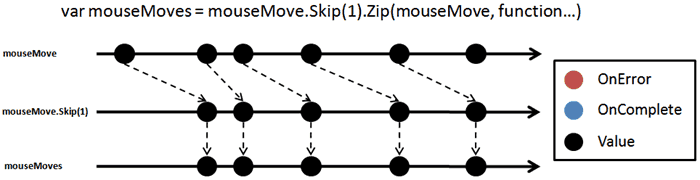
Given a list of values

$latex L \gets 3 \ 8 \ 5 \ 14 \ 34 \ 5 \ 17 \ 21 \ 18$

suppose you want to find the change from one number to the next, i.e. 3 (+5) 8 (-3) 5 (+9) 14…

considering that

$latex 1 \ \downarrow \ L$

=> 8 5 14 34 5 17 21 18

$latex ^-1 \ \downarrow \ L$

=> 3 8 5 14 34 5 17 21

so now you can subtract the two arrays (of equal length) to get the answer:

$latex (1 \ \downarrow \ L) – (^-1 \ \downarrow \ L)$

=> $latex 5 \ ^-3 \ 9 \ 20 \ ^-29 \ 12 \ 4 \ ^-3$

clever, right? It’s reminiscent of the RX approach to tracking mouse moves.

 

mirrors and transposition

You can also pivot data about any direction easily:

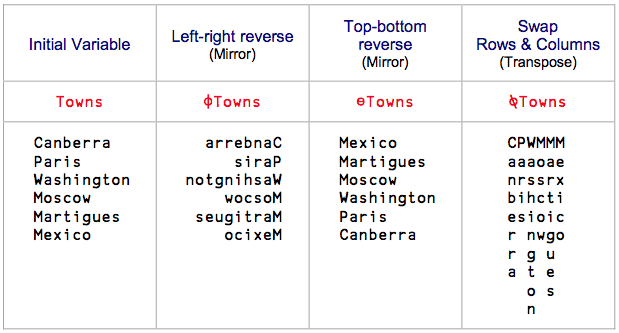
(screenshot taken from Mastering Dyalog APL)

 

outer products

You can use the outer product operator $latex \circ.$ to calculate the cartesian products of two lists:

$latex 1 \ 2 \ 3 \ \circ.\times \ 3 \ 4 \ 5$

=>

$latex

3 \ 4 \ \ 5\\*

6 \ 8 \ \ 10\\*

9 \ 12 \ 15$

using the small circle + dot $latex \circ.$ + an operation to apply, in this case multiply $latex \times$, but could easily be anything else:

$latex 1 \ 2 \ 3 \ \circ.+ \ 3 \ 4 \ 5$

=>

$latex

4 \ 5 \ 6\\*

5 \ 6 \ 7\\*

6 \ 7 \ 8$

here’s even more examples taken from Mastering Dyalog APL:

Unlike some of the operations we’ve seen so far, the outer product operator works across different sized arrays too:

$latex 1 \ 2 \ 3 \ \circ.+ \ 3 \ 4 \ 5 \ 6$

=>

$latex

4 \ 5 \ 6 \ 7\\*

5 \ 6 \ 7 \ 8\\*

6 \ 7 \ 8 \ 9$

 

Finally, there are some common patterns (or idioms) you’ll see in APL.

• find indices in A that exists in B

$latex (A \ \epsilon \ B) \ / \ \iota \rho A$

• find the members (not indices) of A that exists in B

$latex (A \ \epsilon \ B) \ / \ A$

• find indices in A where B first appeared in (i.e. IndexOf)

$latex A \ \iota \ B$

• change the frame of reference

$latex FinalSet[InitialSet \ \iota \ Values]$

• generate indices with incrementing steps

$latex Start + Step \times (\iota Length) – 1$

 

So that’s it, I hope this post has given you a flavour of APL and help you learn the basics quickly. I find the array programming paradigm absolutely mind blowing and a completely different way to think about problems.

Also I find it has a similar transformative effect in changing the way I think about variables – as a point-in-time snapshot of some scalar value – to FRP (e.g. signals in Elm or observables in RX).

 

In the next post, let’s see how we can use APL to solve some simple problems (that’s all I’m able to manage for now!).

 

Links

• Mastering Dyalog APL (free ebook)
• TryAPL
• C# eye for the APL guy