F# – Monty Hall problem

Do you remember that scene from the movie 21 where Kevin Spacey gave our protagonist Ben the game show host problem?

What Kevin Spacey described is known as the Monty Hall problem. It became famous as a question from a reader’s letter to Marilyn vos Savant’s “Ask Marilyn” column in Parade magazine in 1990.

Marilyn’s answer caused quite a bit of controversy at the time and whilst I don’t understand the formal mathematical proof, it’s a problem that can be easily proved through simulations.

 

Simulation with F#

First, let’s set up a few types to represent the problem domain:

Pretty self-explanatory here:

• behind every Door is a Prize;
• the Prize is either a Car or a Goat;
• you Win if you get the Car in the end, otherwise you Lose

When you start a new game you always have three doors, arranged in some random order.

After you had given your initial choice, the game show host will reveal one of the doors that has a Goat?.

Here we have a function that takes in the doors and the player’s initial choice; and return the index of a door that:

1. the player didn’t choose; and
2. has a goat

Putting it together, we have a function that takes in the doors as well as the player’s strategy and return whether the player Win or Lose at the end of the game.

From the code above you can guess the type signature of the strategy function to be int –> int –> int. That is, it takes two integers – the player’s initial choice and the index of the door the host has revealed – and return the player’s final choice.

Now, given the two choices we have – to stay or to change, we can represent it with two strategies:

• strategyA would stay with the player’s original choice;
• strategyB would change

We can now use these two functions to call play with.

p.s. notice we have essentially implemented the Strategy pattern, but without all the boilerplates and interfaces and classes? With just functions! Isn’t that sweet?

 

To be kinder to ourselves, let’s add another helper function that will take in our chosen strategy and run a simulation of 1000 games, and return the number of games that we have won with this strategy:

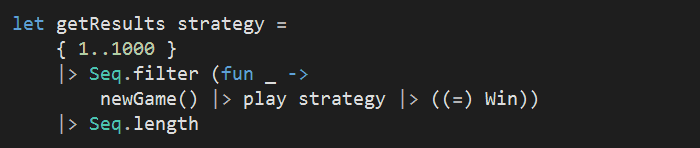
Finally, let’s run our simulations and see how the two strategies perform.

Running this simulation over and over, strategyB consistently outperforms strategyA by roughly 2-to-1, which is exactly what we expected.

You can also just run the simulation yourself on .Net Fiddle here, just click the Run button at the top.

 

Improving our code

Whilst the above is sufficient for its purpose and it’s a pretty short solution, there’re couple of things that can be improved in hindsight:

• player’s choice – to Stay, or Change – is not explicitly represented in the domain;
• whilst a Change can only lead to one outcome – changing to the door that isn’t revealed nor initially chosen – it is expressed implicitly by the logic in strategyB;
• if we were to introduce another strategy (e.g. decide to stay or change randomly) then we’d have to duplicate the logic for change.

To make these improvements is really easy. We can start by adding a type to present the two choices available to the player:

Then we can update the play function to work with it:

So now, our strategy implementations become much simpler:

Again, you can try out this updated version on .Net Fiddle here. It also includes a ‘random’ strategy which chooses to Stay or Change using the rand function we created earlier.

 

There are other things we can improve still. For instance, how do we encapsulate the constraint of having only 3 doors as part of our model?

This way, we can eliminate another invalid state using the type system. I’ll leave that as a teaser to you  and feel free to share your solution in the comments!