Advent of Code F# – Day 24

The source code for this post (both Part 1 and Part 2) is available here and you can click here to see my solutions for the other Advent of Code challenges.

Description for today’s challenge is here.

 

The description for the challenge is quite long and wordy, but ultimately there are only three things we need to remember:

1. the total weight of packages need to be evenly divided into 3 groups
2. the first group needs to have fewest packages possible
3. given the same number of packages (fewest possible), the quantum entanglement (i.e. the product…) of the weights of packages in the first group needs to be the smallest possible

Based on these information, we can have the following:

For my input, all the weights are odd numbers, and the average weight is an even number. Which means we need an even number of packages in each group, furthermore, based on the input the smallest number of packages that can add up to the average weight is 6.

So rather than a brute force approach (which I tried and failed with) we can be smarter and:

1. only consider the first group (since that’s all we need to answer the question)
2. only consider groups of length 6

So, for each package, we will:

• yield the 6-package groups that can be formed with it
• yield the 6-package groups that can be formed without it

and we’ll short circuit a path if after collecting 6 packages in a group but the total weight of the group doesn’t add up to the average.

This is exactly what the following code snippet does, it returns all the 6-package groups that has a total weight equalling the average weight:

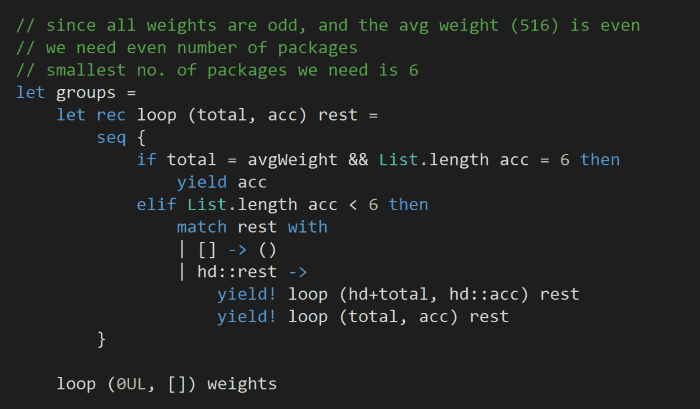
Finally, we just need to find the smallest quantum entanglement value of all the possible combinations:

 

Part 2

Same approach as above, but slightly different setup.

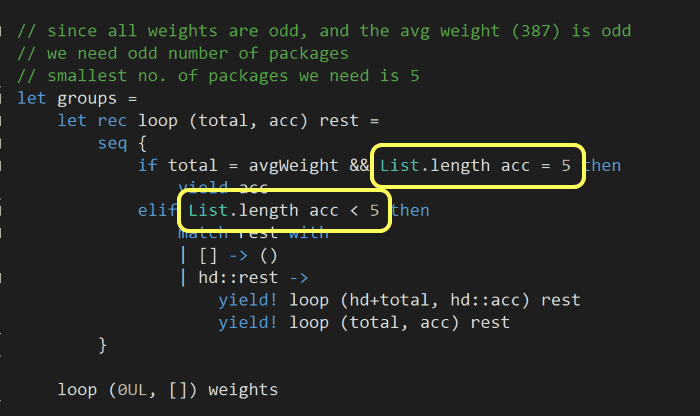
Now that we’re dividing the total weight of all the packages by 4 instead of 3, the average is now an even number – meaning we’ll need an odd number of packages per group. Also, the smallest number of packages per group is now 5: