Project Euler – Problem 75 Solution

The problem description is here, and click here to see all my other Euler solutions in F#.

I based my solution on Euclid’s formula for generating Pythagorean triples.

And given that max L is 1,500,000, the maximum value for m we need to consider is $latex \sqrt{\frac{L}{2}} $. Because $latex L = a + b + c $ and $latex a^2 + b^2 = c^2 $, we can deduce that $latex c < \frac{L}{2} $; and since $latex c = m^2 + n^2 $ we also have $latex m < \sqrt{c} $ and therefore $latex m < \sqrt{\frac{L}{2}} $.

The above makes use of a recursive function to calculate the GCD (based on Euclidean Algorithm):

For efficiency, we’ll create a cache to store the number of ways L can be used to create integer sided right-angle triangle. As we iterate through the m and n pairs we generated above, we’ll take advantage of the fact that if $latex a^2 + b^2 = c^2 $ then $latex ka^2 + kb^2 = kc^2 $ must also be true and increment multiples of L by one.

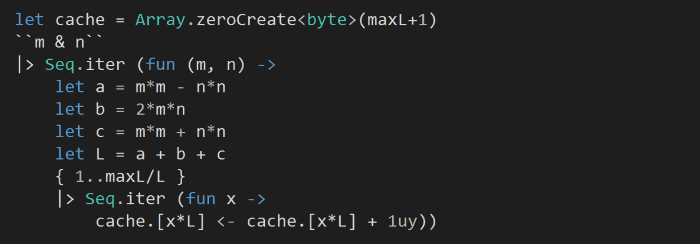
Finally, to work out the answer:

This solution runs for about 350ms on my machine.

The source code for this solution is here.