Project Euler – Problem 11 Solution

Problem

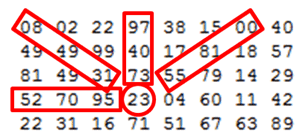
In the 20 x 20 grid below, four numbers along a diagonal line have been marked in red.

08 02 22 97 38 15 00 40 00 75 04 05 07 78 52 12 50 77 91 08

49 49 99 40 17 81 18 57 60 87 17 40 98 43 69 48 04 56 62 00

81 49 31 73 55 79 14 29 93 71 40 67 53 88 30 03 49 13 36 65

52 70 95 23 04 60 11 42 69 24 68 56 01 32 56 71 37 02 36 91

22 31 16 71 51 67 63 89 41 92 36 54 22 40 40 28 66 33 13 80

24 47 32 60 99 03 45 02 44 75 33 53 78 36 84 20 35 17 12 50

32 98 81 28 64 23 67 10 26 38 40 67 59 54 70 66 18 38 64 70

67 26 20 68 02 62 12 20 95 63 94 39 63 08 40 91 66 49 94 21

24 55 58 05 66 73 99 26 97 17 78 78 96 83 14 88 34 89 63 72

21 36 23 09 75 00 76 44 20 45 35 14 00 61 33 97 34 31 33 95

78 17 53 28 22 75 31 67 15 94 03 80 04 62 16 14 09 53 56 92

16 39 05 42 96 35 31 47 55 58 88 24 00 17 54 24 36 29 85 57

86 56 00 48 35 71 89 07 05 44 44 37 44 60 21 58 51 54 17 58

19 80 81 68 05 94 47 69 28 73 92 13 86 52 17 77 04 89 55 40

04 52 08 83 97 35 99 16 07 97 57 32 16 26 26 79 33 27 98 66

88 36 68 87 57 62 20 72 03 46 33 67 46 55 12 32 63 93 53 69

04 42 16 73 38 25 39 11 24 94 72 18 08 46 29 32 40 62 76 36

20 69 36 41 72 30 23 88 34 62 99 69 82 67 59 85 74 04 36 16

20 73 35 29 78 31 90 01 74 31 49 71 48 86 81 16 23 57 05 54

01 70 54 71 83 51 54 69 16 92 33 48 61 43 52 01 89 19 67 48

The product of these numbers is 26 x 63 x 78 x 14 = 1788696.

What is the greatest product of four adjacent numbers in any direction (up, down, left, right, or diagonally) in the 20 x 20 grid?

Solution

open System.IO

let initArray =
    File.ReadAllLines(@"C:\TEMP\euler11.txt")
    |> Seq.map (fun l -> l.Split(' ') |> Seq.map int32 |> Seq.toArray)
    |> Seq.toArray

let height, width = initArray.Length, initArray |> Seq.map (fun l -> l.Length) |> Seq.max
let twoDArray = Array2D.init height width (fun i j -> initArray.[i].[j])

let Up (array2D:int[,]) h w n =
    let lowerBound = h-(n-1)
    let upperBound = h
    if lowerBound < 0 || upperBound > height-1 then []
    else [lowerBound..upperBound] |> List.map (fun y -> array2D.[y, w])

let Left (array2D:int[,]) h w n =
    let lowerBound = w-(n-1)
    let upperBound = w
    if lowerBound < 0 || upperBound > width-1 then []
    else [lowerBound..upperBound] |> List.map (fun x -> array2D.[h, x])

let LeftDiag (array2D:int[,]) h w n =
    let lowerWBound = w-(n-1)
    let upperWBound = w
    let lowerHBound = h-(n-1)
    let upperHBound = h
    if lowerWBound < 0 || upperWBound > width-1 || lowerHBound < 0 || upperHBound > height-1 
    then []
    else
        let wCoordinates = [lowerWBound..upperWBound]
        let hCoordinates = [lowerHBound..upperHBound]
        List.map2 (fun y x -> array2D.[y, x]) hCoordinates wCoordinates

let RightDiag (array2D:int[,]) h w n =
    let lowerWBound = w
    let upperWBound = w+(n-1)
    let lowerHBound = h-(n-1)
    let upperHBound = h
    if lowerWBound < 0 || upperWBound > width-1 || lowerHBound < 0 || upperHBound > height-1 
    then []
    else
        let wCoordinates = [lowerWBound..upperWBound]
        let hCoordinates = [lowerHBound..upperHBound] |> List.rev
        List.map2 (fun y x -> array2D.[y, x]) hCoordinates wCoordinates

let quartets =
    seq { for y in 3 .. width-1 do
            for x in 3 .. height-1 do
                yield Up twoDArray x y 4
                yield Left twoDArray x y 4
                yield LeftDiag twoDArray x y 4
                yield RightDiag twoDArray x y 4
    }

let CalcProduct numbers = numbers |> Seq.fold (fun acc n -> acc * n) 1
let maxProduct = quartets |> Seq.map CalcProduct |> Seq.max

Getting Started

The first thing I needed to do is to get this 20×20 grid of data into F# somehow, and to do so I copied and pasted the grid into a text file C:\TEMP\euler11.txt. File.ReadAllLines will only get us as far as reading the data into a string array though, which still isn’t very useful to us. So in order to get the data into a useful format, I first had to turn this string[] into an int32[][]:

|> Seq.map (fun l -> l.Split(' ') |> Seq.map int32 |> Seq.toArray)

This this line of code takes a line of string such as:

“08 02 22 97 38 15 00 40 00 75 04 05 07 78 52 12 50 77 91 08”

and split it up using the space character, cast each of the string segments into an int32 and return the int32 values as an array.

The next step is entirely optional, in short it converts the int32[][] (that is, an array of int32 arrays) into a int32[,] (a 2-dimensional array). The main difference between a normal Array and an Array2D is how you access its member elements – Array.[x].[y] versus Array2D.[x, y].

The Interesting Bits

Now, to find the answer you can iterate through each element in the 2 dimensional array and for each element calculate the product of each 4 adjacent numbers centred around that element (see image on the left) and find the max product.

However, this approach introduces a large amount of duplicates. For instance, the right pattern from 28 gives [28; 66; 33; 13] which yields the same product as the left pattern from 13.

You can cut down on the number of duplicates by only processing the first 4 patterns, shown in red. For each of the patterns I have created a corresponding function which takes a 2D array, a height and width value which identifies the element in the 2D array, a number which indicates the number of adjacent numbers that make up the pattern, and returns the int32 array.

There are some edge cases of course, take the element at (0, 0) position for instance, there aren’t enough elements in any of the directions to fill up the patterns. In these cases, the functions will simply return an empty array. This also means that there is no need to consider any of the elements whose x (horizontal) and z (vertical) coordinates is less than 3.

The Finishing Touch

The final step involves getting a sequence of all the 4-number arrays generated by the aforementioned patterns, I have chosen to use yield and put the results into a sequence:

quartets;;
val it : seq<int list> =
seq
[[97; 40; 73; 23]; [52; 70; 95; 23]; [8; 49; 31; 23]; [23; 55; 81; 0]; ...]

And for each array work out its product (using the CalcProduct function) and then find the greatest product in the array.