
Yan Cui
I help clients go faster for less using serverless technologies.
This article is brought to you by

The real-time data platform that empowers developers to build innovative products faster and more reliably than ever before.
Problem
Starting in the top left corner of a 2×2 grid, there are 6 routes (without backtracking) to the bottom right corner.
How many routes are there through a 20×20 grid?
Solution
let rec factorial(n:bigint) = if n <= 1I then 1I else n * factorial(n-1I) let combo n k = factorial(n) / (factorial(k) * factorial(n-k)) let answer = combo 40I 20I
It took me a while to figure out that this problem is actually a simple combination problem – consider a X by Y grid, any route from the top left to the bottom right corner without backtracking must have travelled Right X number of times and Down Y number of times. In the case of the original example:
RRDD, RDRD, RDDR, DRRD, DRDR, DDRR
This also means that all routes have a total of X + Y steps, and the number of routes is equal to the number of ways you can pick X number of R moves out of X + Y, i.e.
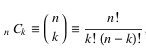
where n = X + Y and k = X.
Whenever you’re ready, here are 4 ways I can help you:
- Production-Ready Serverless: Join 20+ AWS Heroes & Community Builders and 1000+ other students in levelling up your serverless game. This is your one-stop shop for quickly levelling up your serverless skills.
- Do you want to know how to test serverless architectures with a fast dev & test loop? Check out my latest course, Testing Serverless Architectures and learn the smart way to test serverless.
- I help clients launch product ideas, improve their development processes and upskill their teams. If you’d like to work together, then let’s get in touch.
- Join my community on Discord, ask questions, and join the discussion on all things AWS and Serverless.

let p15 =
let factorial n = [1I..n] |> List.fold (*) 1I
factorial(2I*20I)/(factorial(20I) ** 2)