Project Euler – Problem 67 Solution

Problem

By starting at the top of the triangle below and moving to adjacent numbers on the row below, the maximum total from top to bottom is 23.

 

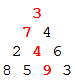
That is, 3 + 7 + 4 + 9 = 23.

Find the maximum total from top to bottom in triangle.txt (right click and ‘Save Link/Target As…’), a 15K text file containing a triangle with one-hundred rows.

NOTE: This is a much more difficult version of Problem 18. It is not possible to try every route to solve this problem, as there are 2⁹⁹ altogether! If you could check one trillion (10¹²) routes every second it would take over twenty billion years to check them all. There is an efficient algorithm to solve it. ;o)

Solution

open System.IO

// covers the data in the text to a triangle of ints, i.e. int list list
let triangle =
File.ReadAllLines(@”C:\TEMP\triangle.txt”)
|> Array.map (fun s -> s.Split(‘ ‘) |> Array.map int32 |> Array.toList)
|> Array.toList

// function to return all the combinations of n elements from the supplied list
let rec comb n list =
match n, list with
| 0, _ -> [[]]
| _, [] -> []
| k, (x::xs) -> List.map ((@) [x]) (comb (k-1) xs) @ (comb k xs)

// calculates the next row in the T triangle given the new row in R and the last row in T
let getNewTotal (row:int list) (total:int list) =
let head = total.Head
let tail = List.nth total (total.Length-1)
let body = total |> Seq.windowed 2 |> Seq.map (fun l -> Seq.max l) |> Seq.toList

List.map2 (+) row (List.concat [[head]; body; [tail]])

// recursively traverse down the R triangle and return the last row in T
let rec traverse (raw:int list list) (total:int list) n =
let row = raw.[n]
let newTotal = getNewTotal row total

if n < (raw.Length-1) then traverse raw newTotal (n+1) else newTotal let answer = List.max (traverse triangle [59] 1) [/code] See problem 18 solution for the full explanation of this solution.