Yan Cui
I help clients go faster for less using serverless technologies.
This article is brought to you by
Don’t reinvent the patterns. Catalyst gives you consistent APIs for messaging, data, and workflow with key microservice patterns like circuit-breakers and retries for free.
Problem
By starting at the top of the triangle below and moving to adjacent numbers on the row below, the maximum total from top to bottom is 23.
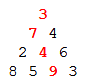
That is, 3 + 7 + 4 + 9 = 23.
Find the maximum total from top to bottom of the triangle below:
NOTE: As there are only 16384 routes, it is possible to solve this problem by trying every route. However, Problem 67, is the same challenge with a triangle containing one-hundred rows; it cannot be solved by brute force, and requires a clever method! ;o)
Solution
With the warning of problem 67 in mind, I set out to tackle this problem with a somewhat efficient solution which will also work for problem 67. To start off, let’s look at the simple example, as you traverse down the triangle from the top you have two options at every turn – go left, or go right. From the third row onwards, some of the paths will end up in the same place in the triangle:
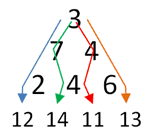
From the above image you can see that the path 3-7-4 and 3-4-4 both exit the mini triangle at the same location but carrying two different totals – green = 14, red = 11. If you were to continue down the triangle from this point on, regardless of whether you’re going to turn left or right in the next move, the max total will surely have to come from the path which has generated the highest total so far.
If we apply the same logic to the entire triangle we can build up a triangle of totals for the raw triangle where every element represents the max total achievable by any path that has lead to it:
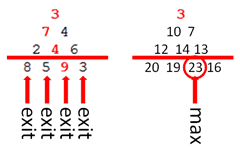
Let’s call this triangle of totals T, and the original triangle R, we have:
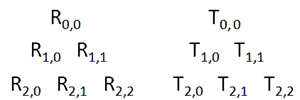
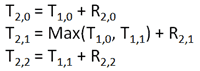
You can see that T(2,1) differed from T(2,0) and T(2,2) in that it required us to find the greater between T(1,0) and T(1,1). For simplicity sake, let’s say that for a given row n, in T (where n >= 2) we have:
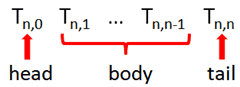
The max total from top to bottom of the triangle R is equal to the max total in the last row of the triangle T. Seeing as we’re only interested in the max total rather than the triangle T itself, my solution below only returns the last row of T which is all we need to solve the problem:
Whenever you’re ready, here are 3 ways I can help you:
- Production-Ready Serverless: Join 20+ AWS Heroes & Community Builders and 1000+ other students in levelling up your serverless game. This is your one-stop shop for quickly levelling up your serverless skills.
- I help clients launch product ideas, improve their development processes and upskill their teams. If you’d like to work together, then let’s get in touch.
- Join my community on Discord, ask questions, and join the discussion on all things AWS and Serverless.
Pingback: Project Euler — Problem 67 Solution | theburningmonk.com
why does it seem so complicated.
Pingback: Project Euler–Problem 81 Solution | theburningmonk.com
here’s my solution, basically I do the same thing but I start from the bottom of the triangle
open System.IO;
let getMaxSum (triangle: int list list) =
. let getResLine currLine prevLine =
. let rec loop resLine prevLine’ = function
. |[] -> resLine
. |hd::tl -> loop ((hd + (max (List.nth prevLine’ 0) (List.nth prevLine’ 1)))::resLine) (List.tail prevLine’) tl
. loop [] prevLine currLine |> List.rev
. let rec loop (prev:int list) (tri: int list list) =
. match tri with
. | [] -> prev.Head
. | hd::tl -> loop (getResLine hd prev) tl
. loop triangle.Head triangle.Tail
let triangle n =
. File.ReadAllLines(@”C:\euler\”+n+”.txt”)
. |> Array.map (fun s -> s.Split(‘ ‘) |> Array.map int32 |> Array.toList)
. |> Array.toList
. |> List.rev
let p18 = getMaxSum (triangle “18”)
let p67 = getMaxSum (triangle “67”)
I tried to put dots, in order to get indentation, but it didn’t really work, changing the font-family to Courier New for the comments will fix that