Project Euler – Problem 72 Solution

Problem

Consider the fraction, n/d, where n and d are positive integers. If n<d and HCF(n,d)=1, it is called a reduced proper fraction.

If we list the set of reduced proper fractions for d <= 8 in ascending order of size, we get:

1/8, 1/7, 1/6, 1/5, 1/4, 2/7, 1/3, 3/8, 2/5, 3/7, 1/2, 4/7, 3/5, 5/8, 2/3, 5/7, 3/4, 4/5, 5/6, 6/7, 7/8

It can be seen that there are 21 elements in this set.

How many elements would be contained in the set of reduced proper fractions for d <= 1,000,000?

Solution

let hasDivisor(n) =
    let upperBound = bigint(sqrt(double(n)))
    [2I..upperBound] |> Seq.exists (fun x -> n % x = 0I)

let isPrime(n) = if n = 1I then false else not(hasDivisor(n))

// define the sequence of prime numbers
let primeSeq =
    Seq.unfold (fun state -> if state >= 3I then Some(state, state+2I) else Some(state, state+1I)) 1I
    |> Seq.filter isPrime |> Seq.cache

// define function to find the prime denominators for a number n
let getPrimeFactors n =
    let rec getPrimeFactorsRec denominators n =
        if n = 1I then denominators
        else
            let denominator = primeSeq |> Seq.filter (fun x -> n % x = 0I) |> Seq.head
            getPrimeFactorsRec (denominators @ [denominator]) (n/denominator)
    getPrimeFactorsRec [] n

let totient n =
    let primeFactors = getPrimeFactors n |> Seq.distinct
    n * (primeFactors |> Seq.map (fun n' -> n'-1I) |> Seq.reduce (*)) / (primeFactors |> Seq.reduce (*))

let f n = [2I..n] |> List.map totient |> List.sum
let answer = f 1000000I

This is almost identical to the solution to problem 69, with the exception of the last two steps. According to the information on Farey sequence on wikipedia:

The Farey sequence of order n contains all of the members of the Farey sequences of lower orders. In particular F_n contains all of the members of F_n?1, and also contains an additional fraction for each number that is less than n and coprime to n. Thus F₆ consists of F₅ together with the fractions ¹?₆ and ⁵?₆. The middle term of a Farey sequence F_n is always ¹?₂, for n > 1.

From this, we can relate the lengths of F_n and F_n?1 using Euler’s totient function ?(n) :

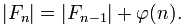
Given that F1 = 0 in our case, F2 = 0 + totient 2, F3 = totient 2 + totient 3, and so on, and therefore Fn = totient 2 + totient 3 + … totient n.