
Yan Cui
I help clients go faster for less using serverless technologies.
Problem
A number chain is created by continuously adding the square of the digits in a number to form a new number until it has been seen before.
For example,
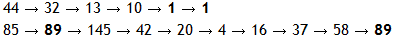
Therefore any chain that arrives at 1 or 89 will become stuck in an endless loop. What is most amazing is that EVERY starting number will eventually arrive at 1 or 89.
How many starting numbers below ten million will arrive at 89?
Solution
let max = 10000000
// build up a cache for all the numbers from 1 to 10 million
let cache = Array.init (max+1) (fun n ->
match n with
| 0 | 1 -> Some(false)
| 89 -> Some(true)
| _ -> None)
// define function to add the square of the digits in a number
let addSquaredDigits n =
n.ToString().ToCharArray()
|> Array.sumBy (fun c -> pown (int(c.ToString())) 2)
// define function to take an initial number n and generate its number chain until
// it gets to a number whose subsequent chain ends with 1 or 89, which means that
// all previous numbers will also end in the same number
let processChain n =
let rec processChainRec n (list: int list) =
if cache.[n] = None then processChainRec (addSquaredDigits n) (list@[n])
else list |> List.iter (fun n' -> cache.[n'] <- cache.[n])
processChainRec n []
// go through all the numbers from 2 to 10 million using the above function
[2..10000000] |> List.iter processChain
// how many numbers whose number chain ends with 89?
let answer = cache |> Array.filter (fun n -> n = Some(true)) |> Array.length
This is actually a fairly simple problem, with the main challenge being how to make it run fast enough to obey with the one minute rule which is where the cache comes in.
Using the property that if a chain starting with the number n, i.e. n, n1, n2, …, ends in 89 then the chain starting with any of the numbers n1, n2, … will also end in 89 we can minimise the amount of computation required by caching previous results. Note I didn’t have to mark the cache as mutable in this case because the Array construct in F# is a fixed-sized, zero-index, mutable collections of elements.
Whenever you’re ready, here are 3 ways I can help you:
- Production-Ready Serverless: Join 20+ AWS Heroes & Community Builders and 1000+ other students in levelling up your serverless game. This is your one-stop shop for quickly levelling up your serverless skills.
- I help clients launch product ideas, improve their development processes and upskill their teams. If you’d like to work together, then let’s get in touch.
- Join my community on Discord, ask questions, and join the discussion on all things AWS and Serverless.

I do not understand why my program is about 15 seconds slower than your program:
//same as addSquaredDigits except takes 15 seconds less to compute
let sosd x = x.ToString().ToCharArray() |> Array.map (fun i -> (int i) – (int ‘0’)) |> Array.map (fun i -> int ((float i)**(float 2))) |> Array.sum
//recursively checks to if the sum of the squared digits of n is 89 and returns true if so
let rec p (n) =
let o = sosd n
if o = 89 then true
elif o = 1 then false
else p (o)
//number of converges at 89
let t = [1..9999999] |> List.filter(fun i -> p i) |> List.length
Good question, when I ran your solution (26.282s) vs mine (22.565s) they were within 4s of each other, although when I substituted ‘addSquaredDigits’ with your version it cut my solution’s run time to 12.713s and there’s a solid 10s difference directly attributable to how I summed the squared digits.
My initial assumption was pown vs ** but that wasn’t it:
let nums = [2..10000000] |> List.map (fun n -> n % 10)
> nums |> List.map (fun n -> pown n 2);;
Real: 00:00:01.528, CPU: 00:00:01.326, GC gen0: 27, gen1: 25, gen2: 1
> nums |> List.map (fun n -> n * n);;
Real: 00:00:00.890, CPU: 00:00:00.780, GC gen0: 26, gen1: 23, gen2: 1
some minor difference, not enough to account for the 10s difference.
So maybe it’s the conversion from char to int to squared?
First thing I noticed was that it takes a little while just to get the char array back
> let l = [2..10000000] |> List.map (fun x -> x.ToString().ToCharArray());;
Real: 00:00:07.336, CPU: 00:00:06.879, GC gen0: 169, gen1: 112, gen2: 3
and to turn each char into a string took so long I gave up after a minute or so, but in my solution the caching means it didn’t have to do the conversion for every number.
So I’d say the culprit in my solution is the char.ToString(), but having a cache would still be useful in any case. And in FP, there’s the well known technique of memoization, so with that in mind, this solution :
https://gist.github.com/theburningmonk/d491e98da165c6de180d
cuts up the repeated work of calculating squared digit from char, as well as recalculating previous results of n.
Now it runs in 11.380s
As an experiment, if I change squareDigit to:
let squareDigit (c : char) = pown (int(c.ToString())) 2
(i.e. removing the memoization) then the runtime went back to 21.558s.
So there, char.ToString() is the reason why there’s such a noticeable difference between the two solutions.
Wow, thank you for responding really quickly! I know understand why your program is much faster: During your processChain function, if a certain number converges or reaches 89, you are storing each element of its chain in the cache list because all of the numbers in the chain that converges to 89 also converge to 89. This is faster (especially as the numbers get larger) because you would not have to recalculate the chain of a number if it was already contained in a chain. Whereas in my solution, it is pure bruteforce. Thanks for posting this explanation of your solution and your explanation as to why the addSquaredDigits function took longer than my sosd function!
Not a problem, was good for me to find out something so trivial as to char.ToString() can be so costly in this case. It was also good exercise for me to go back and optimise this solution too, thank you for that :-)
//here’s one about 15 times faster:
open System
open System.Diagnostics
let t0 = new Stopwatch()
t0.Start()
let max = 10000000
// define function to add the square of the digits in a number
let inline square (x:int) : int = x*x
let addSquaredDigits (n:int) : int =
let rec go s x = if x = 0 then s else go (s + square(x % 10)) (x / 10) in go 0 n
// build up a cache for just the first 568 or so numbers
let cache = Array.init (addSquaredDigits (max-1) + 1) (fun n -> match n with | 0 | 1 -> Some(false) | 89 -> Some(true) | _ -> None)
let processChain n =
let rec processChainRec n (list: int list) : bool option=
if cache.[n] = None then processChainRec (addSquaredDigits n) (list@[n])
else
list |> List.iter (fun n’ -> cache.[n’] <- cache.[n])
cache.[n]
processChainRec (addSquaredDigits n) []
// go through all the numbers from 2 to 10 million using the above function
let mutable answer = 0
for i = 2 to max do
answer 1 | _ -> 0
printfn “Answer=%d, %d ms” answer t0.ElapsedMilliseconds
can you put this in a gist? I think there’s some copy error here:
answer 1 | _ -> 0
looks like a match … with clause got chopped off
https://github.com/tallpeak/euler92/blob/master/euler92b.fsx
Nice, on my laptop, my solution runs at around 16s. Your change in `addSquaredDigits` (not using ToString()) shaved about 10s off the time, then using structs for cache shaved off another 3s or so.
So I guess the other 2.x seconds comes from working against a much smaller number of items, though I don’t understand how you got 568 from (clearly don’t understand the problem as deeply as you do ;-) )
after the first iteration of sumSquaredDigits (or addSquaredDigits), any 7 digit number will be converted to, at max, (9*9*7) = 567, so the cache is small and fast to generate if you make it only for the numbers 0 to 567. (sumSquaredDigits 9999999 = 567). And after generating that cache, a single call to sunSquaredDigits per number and and a simple index into the cache are all that is needed. There’s also a pure combinatorial (mathematical) solution I’ve read various places, but I found this problem more interesting for benchmarking and comparing naive approaches in various languages, pretending I’m too bad at math to think of the combinatorial solution (and maybe I am…) Ideally, building the cache from 0..999, as in my Scala version, would allow for making a faster sumSquaredDigits function that could just split the number (up to 999,999,999) into three sections, look up the ssd cache value for each of those sections, then sum them, for a slight additional speedup. Using this technique, I think my assembly version takes 20 to 50 ms. (Clearly, I got carried away on this little exercise, two years ago.)
ah I see, thanks for explaining that, makes a lot of sense now. Do you have a link to the pure combinatorial solution to this problem? You’ve piqued my curiosity :-)
The 568 items in the cache comes from only caching the second iteration, and always performing sumSquareDigits once on each of the big numbers, then looking up the answer for the chain after that. Building the cache to 10 million is just too time-consuming. I could have also used the technique of caching all sumSquaredDigits from 0..999, as I did in the Scala and assembly versions. My assembly version got down to under 10 ms using that technique (i5-4300U, average of 1000 timings=9.1 ms.) (Maybe I’ll write a factorcode version next.)
http://www.mathblog.dk/project-euler-92-square-digits-number-chain/