Elm – fun with L-System (Part 1)

Friday was my last day at Gamesys, bringing to an end a wonderful 6 years I’ve enjoyed at the company. Seeing as I’m starting my new job at JustEat in November, so for the first time in almost 10 years I have time on my hands to relax and go through my backlog of TODOs.

One of those outstanding TODOs was to check out L-System, which I’ve been fascinated about ever since I read this post by Mathias Brandewinder.

 

I wanted to try out the same examples in Elm, which is another hobby of mine.

Why?

Because it has this awesome time-travelling debugger, which I can use to see how the different examples grow frame by frame and then even go back and forth!

 

Series:

1. Algae (this)
2. Pythagoras Tree
3. Cantor Dust
4. Koch Curve
5. Sierpinski Triangle
6. Dragon Curve
7. Fractal Plant

 

As the wikipedia page for L-System contains quite a few different examples, I’ll go through the implementation for each in Elm over a few posts.

To start nice and easy, let’s look at the Algae example.

 

Modelling a L-System

Since there’s no drawing involved, this example allows us to focus on modelling a L-System with types.

As you can see, my approach here is almost identical to Mathias’s, with the exception that Symbol is a type alias for Char rather than a union type of its own right.

Why?

Mostly because you can’t use a union type as key in a Dict in Elm. But also because I find it simplifies consuming code in this case, whilst a type alias still allows me to surface my domain through types.

Personally I’ve used both approaches and make my choice based on the chance of getting it wrong (or, what additional type safety buys me) and the amount of effort involved.

p.s. Scott Wlashcin wrote a nice piece about the 2 approaches from a performance point-of-view, which I also recommend you reading.

 

Then we just need a way to “evolve” a state based on the rules of a L-System:

Since Dict.get returns a Maybe,  we have to provide a default value – the symbol itself in this case – if the symbol is not found in the rules.

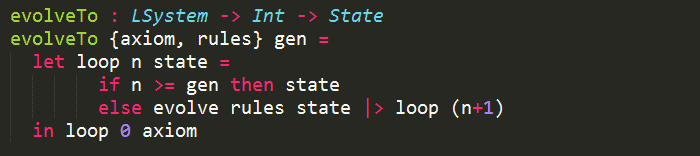
To evolve the L-System to a given generation, we can just use simple recursion:

 

Modelling the Signals

For the demos, I want to be able to go from generation to generation using the arrows keys.

e.g. starting with gen 0, -> moves to gen 1, -> again moves to gen 2. But if you press <- then you move back to gen 1, and so on.

To do that, we need to capture the arrow key presses, and use the x value (see mapping below) to “change” the current generation.

Starting with gen 0 (the axiom), we’ll fold over the signal of integer values (either -1 for LEFT, or +1 for RIGHT), whilst capping the output value at 0 (hence the max 0 at the end).

Finally, we’ll map this signal of generation numbers into a signal of states by evolving the L-System to the specified generation:

 

All the code we’ve seen above are put inside a Core module that all the other examples will share.

 

Example 1 : Algae

So now we can finally look at one of the L-System examples. Once the Core module is in place, there’s actually not much to be done here.

We still need to define the L-System for Algae:

but since there’s nothing to be drawn on the screen, we’ll just keep things simple and display the output (list of Char) as a string instead:

 

Live Demo (here)

Remember, use LEFT and RIGHT arrow keys to evolve/devolve the L-System.

 

Source Code (here)

 

Next : Pythagoras Tree

 

Links

• Fun with L-system (with F#)
• L-System wikipedia
• Elm’s online editor
• Source code for this post
• Live demo