Elm – fun with L-System (Part 3)

Series:

1. Algae
2. Pythagoras Tree
3. Cantor Dust (this)
4. Koch Curve
5. Sierpinski Triangle
6. Dragon Curve
7. Fractal Plant

Last time out we implemented the Pythagoras Tree example from the L-System wikipedia page. Now, let’s continue our journey and see how we can implement the Cantor Dust example in Elm.

Example 3 : Cantor Dust

First, let’s define our L-System:

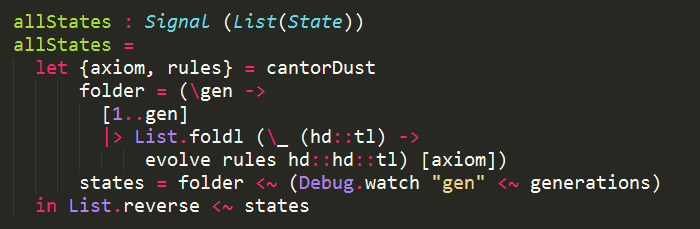
The interesting thing about this example is that we need to draw, not only the current generation, but also all the preceding generations too.

So I had to approach things slightly differently, and instead of dealing with a Signal(State), I need a Signal(List(State)):

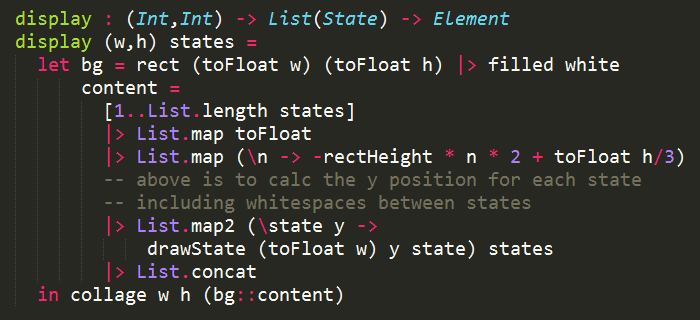
This signal of List(State) is then passed to the display function (along with the dimension of the window):

 

We can use rectangle to represent the individual bars, and for my screen 25 pixels seems to be a good height.

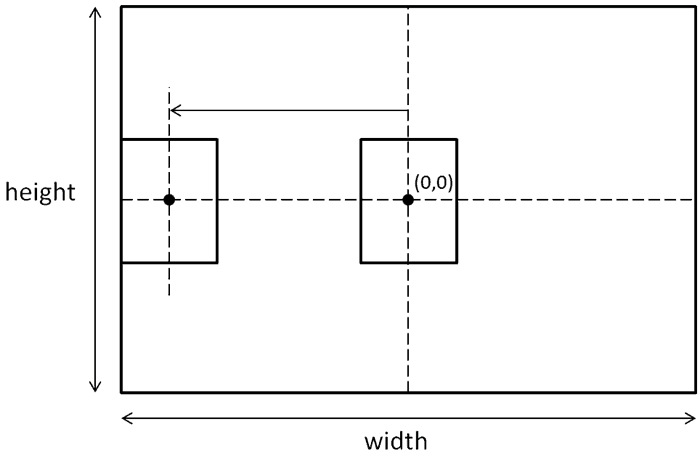
For each generation we want to place them some distance apart. That is to say that the state for each generation should have a stepped Y position.

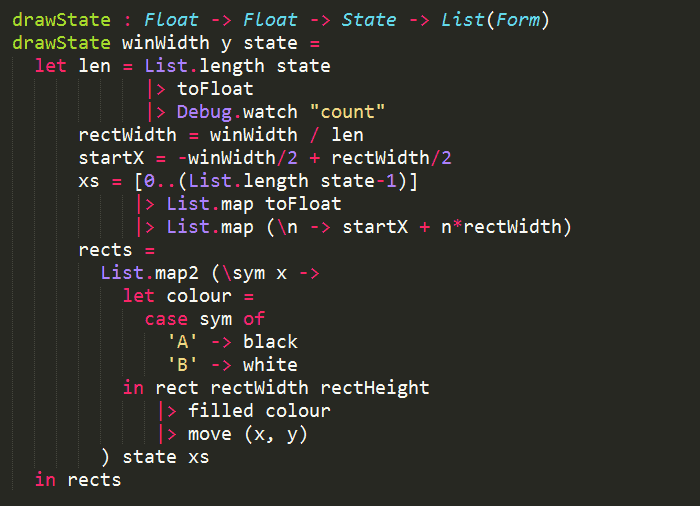
so now, we need to add a drawState function that will take in:

• the width of the window;
• the y position for its rectangles; and
• the state it needs to draw

and return a list of rectangles for that state.

You may remember the following paragraph from Part 2:

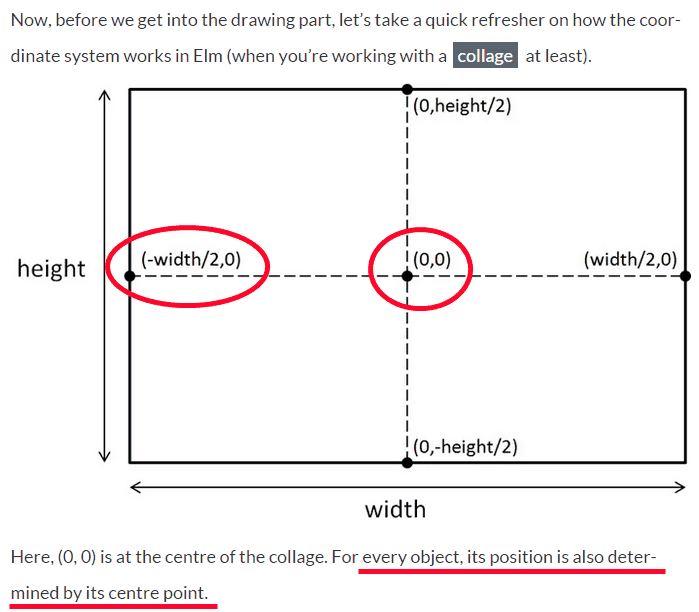
So to work out the x positions of the first rectangle for this state, we have this slightly dubious looking line of code:

and the next block of code generates the x positions for all the rectangles:

 

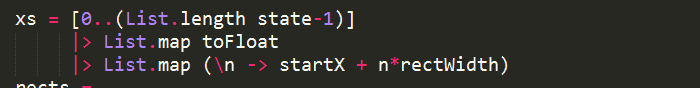
Running this example in Elm Reactor I can get the demo to gen 8, after that it takes noticeably longer to render and the bars are so thin that they’re barely visible.

 

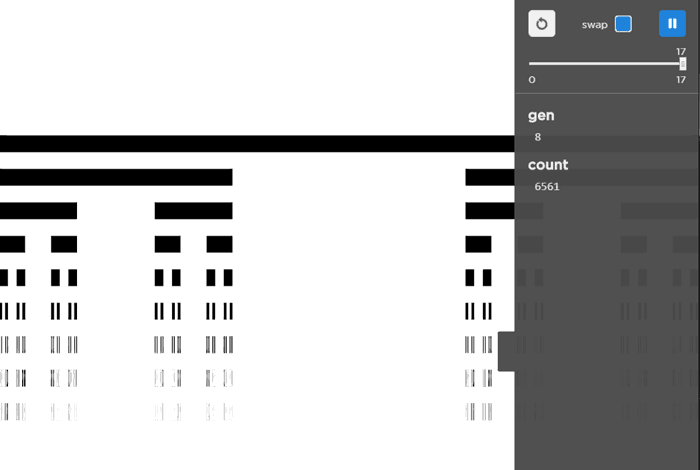
Live Demo (here)

Use LEFT and RIGHT arrow keys to evolve/devolve the L-System.

 

Source Code (here)

 

Next : Koch Curve

Links

• Source code for this post
• Live demo